今回はディープラーニングにおいては重みを更新する際に用いられる誤差逆伝播法(バックプロパゲーション)という手法について解説します。前回までに説明したディープラーニング・ニューラルネットワーク・パーセプトロン・活性化関数については以下を参照ください。
ニューラルネットワークにおける勾配降下法
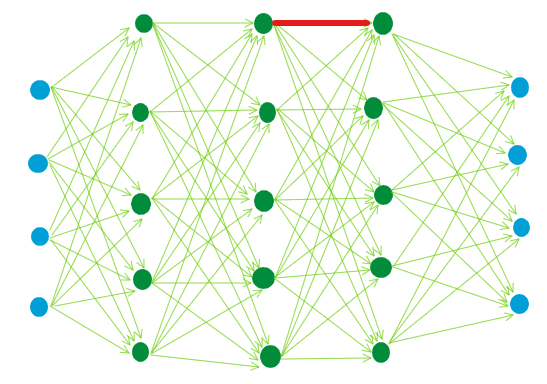
以下の図はニューラルネットワークの記事で掲載した図です。
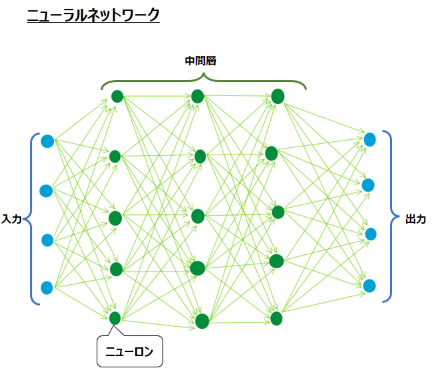
ニューラルネットワークにおいては上図の矢印1つひとつが重みパラメータです。これらの値をどうするかを決めるのに、勾配降下法を用います。勾配降下法では微分によって勾配を算出し、それに基づいて重みをどのように更新するかを決めます。勾配降下法については以下の記事を参照ください。
では具体的に、例えば以下の赤い矢印の重みを更新するにはどうすればよいかと考えてみます。
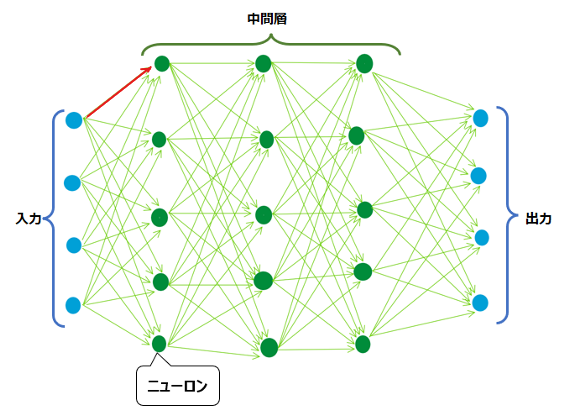
微分、つまりこの赤い矢印が少し変化した時に出力と正解の誤差がどのくらい変わるかを調べるには、何とその先の青枠内のすべての部分について計算し直さないといけません。赤い矢印が変化したら、その先もすべて何らか変化が生じ、誤差の値に影響を与えるため、赤い矢印の変化による誤差の変化を計算するには、その先の工程(青枠)も計算し直す必要があるのです。
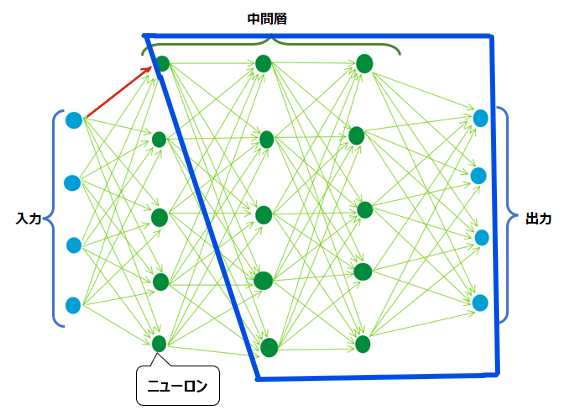
上の図のように、矢印(重み)1本について考えるだけでも微分の計算コストが高い(計算量が多くてPCが大変)ですが、勾配降下法においてはすべての重みについて微分の作業を行わないと、更新ができません。上のような単純な構図であっても、すべての重みについて微分する計算コストがどれほど高いか容易に想像がつくかと思います。さらに、ディープラーニングにおいては入力と出力が10,000個、中間層も数100層存在するようなことがあります。これらの計算コストは果てしなく高くなります。
そこで使用されるのが、誤差逆伝播法(バックプロパゲーション)です。
誤差逆伝播法(バックプロパゲーション)
誤差逆伝播法(Backpropagation、バックプロパゲーション)は、直感的に説明するのが非常に困難です。かといって、数式を用いて説明すると文系の人には全く理解できなくなってしまいますので、ここでは簡単な説明にとどめます。
前項で説明した通り、ニューラルネットワークの重みが数万個あるような場合に全てまともに微分を計算するのは大変です。そこで誤差逆伝播法では、微分の計算式を式変形することで計算しやすくします。
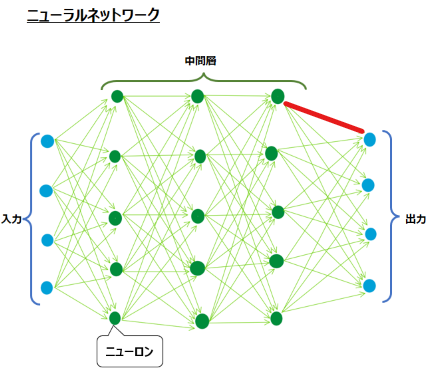
まずは出力層に向かう重みの更新だけを考えます。数式は掲載しませんが、変数(更新されるので値が変化する)である重みを除いて考えると、①中間層にある緑の値と、②出力層における活性化関数、そして③正解値がわかれば、誤差が計算できます。
簡単に文字で表すと以下の通りです。
予測値 = (①緑の値 x 重み(変数)) に②活性化関数を適用した値
誤差 = 予測値と③正解値の差
①~③の数値がわかれば、変数である重みが変化したときに誤差がどのように変化するのかがわかることがイメージできるのではないでしょうか。
言い換えると、上図の赤い矢印の重みの勾配(重みが少し変化した時の誤差の変化量)の計算をするには、重みを変数とし、①②③が規定値である関数と考えることができます。
①②③が規定値であるというのがよくわからないかもしれません。ここでイメージしてほしいのは、重みを更新するということは、1度重みを規定値又はランダム値によって決めたうえで、すべての層で入力と重みの掛け算が計算が実行され、活性化関数も適用され、誤差が計算された後の状態であるということです。入力層の値は自分の用意したデータを使い、重みに例えば初期値としてすべて”1″を設定したとします。中間層で使用する活性化関数も例えばSigmoid関数など予め設定していますから、全ての中間層と出力層の値も何らか決まり、出力層の値が予測値となります。結果、正解値と予測値の誤差が計算されます。初めはイメージし難いですが、ディープラーニングの重みの更新というのは、上述のプロセスを一通り実行した後に行われるということを念頭におくと、理解が進むかもしれません。
具体的に数値をあてはめてみましょう。例えば赤い重みの入力になっている緑の中間層の値が0.7で、重みが0.1だったとします。この時出力層では、まず中間層の0.7と重みの0.1が掛け算され、0.07となります。出力層における活性化関数がシグモイド関数であれば、出力値は1/1+exp(-x)より、0.517となります。もし正解値が0であれば、二乗誤差は0.268となります。


出力層における勾配が簡単に計算できそうなことがイメージできるのではないでしょうか。これが、出力層に向かう重みの更新は、変数である重みと、規定値である①中間層にある緑の入力値②出力層における活性化関数③正解値の関数である、ということの意味です。
これをさらに言い換えれば、重みが少し変化した時の誤差の変化量は、①③の値や②の数式の結果としての予測値によって算出ができるということです。上図でいえば、重みを0.1=>0.15に変化させると誤差が増えてしまっていることが見て取れます。これが、数学的には微分の連鎖率を使った式変形の言語的な説明です。詳細な数式は割愛しますが、連鎖率という計算手法を用いることで、重みが少し変化した時の誤差の変化量を求めるための微分の式を、入力値と予測値と正解値によって簡単に計算できる式に変形することができるのです。
上述の微分の連鎖率による式変形を用いて、中間層における重みの更新を考えます。例えば以下の場所の重みを更新するとします。上述の出力層の青色に向かう重みが全て更新し終わった前提とします。
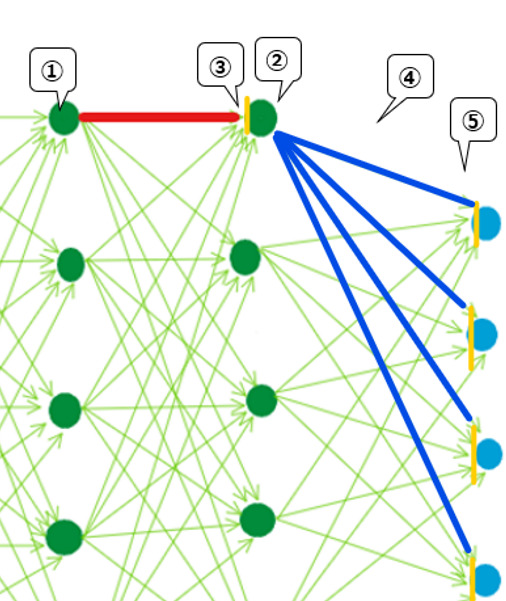
この場合は、以下の拡大図のように、①左側の緑の値と、②右の緑の値を③重み付き和(黄色)で微分した値と、④その更に先の重み(青線)と、⑤誤差をその先の重み付き和(黄色)で微分した値によって求めることできます。ここは直感的な説明が不可能なので、数学のルールの従って式を変形したら、たまたま計算のしやすい形にすることができた、と理解してもらえると良いかと思います。

ではなぜこうすると計算しやすいのかというと、上述の①〜⑤が全て既に計算されている値だからです。①②③は一度プロセスを回した値を使えますし、④⑤は、先述の出力層の重み更新作業によって計算が完了しています。
纏めると、まず出力層では式変形によって微分の計算を簡略化し、中間層では出力層の簡略版微分の値を用いて新たな複雑な計算をせずに微分を計算することができます。
このように、微分の計算を式変形によって簡略化し、また出力層から入力層に向かって後ろから計算していくことで計算コストを下げる方法のことを、誤差逆伝播法と呼びます。
順伝播と逆伝播
順番が前後するようですが、最後に順伝播と逆伝播という言葉についても整理します。
順伝播
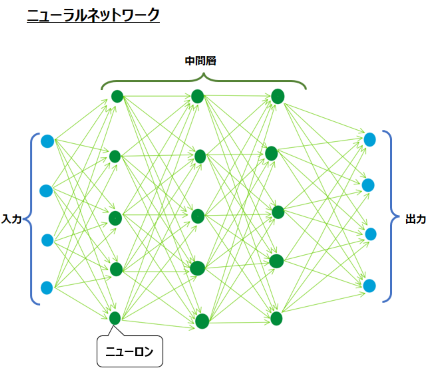
ニューラルネットワークにおいては、入力データに重みをかけ、その重み付き和に活性化関数を適用した出力値を新たな入力値として次の層に渡し、最終的には出力層での出力を予測値とし、正解値との誤差を計算します、以下の図でいえば左から右に向かうこの流れを、順伝播と呼びます。
逆伝播
一方誤差逆伝播の項目で説明した通り、重みの更新においては出力層から中間層に向けて損失関数の微分(の式を変形したもの)を計算することで、効率的に全ての重みを更新することができます。この順序が、上述の順伝播と逆の流れを辿っていることから、逆伝播と呼ばれているのです。


コメント