【機械学習】勾配降下法とは何か

今回は勾配降下法について説明します。勾配降下法とは、機械学習のモデルにおいて損失関数を最小とするような最適なパラメータを設定するためのアルゴリズムです。勾配降下法を理解するためには、まずは損失関数(誤差関数)というのが何かを理解する必要があります。損失関数については前回の記事を参照してください。

機械学習の流れ
重みパラメータwの更新方法
勾配降下法の問題と様々な種類

機械学習の流れ

前回記事でも説明した機械学習のプロセスは重要なのでここで再掲します。

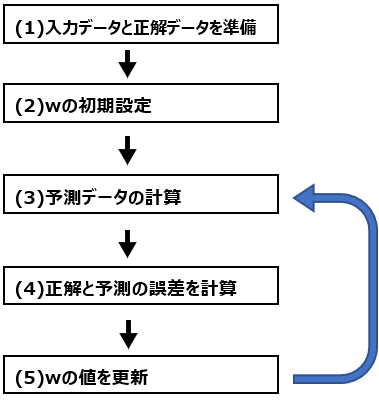
前回記事でも説明した通り、機械学習における変数は重みパラメータｗだけです。入力データと正解データは既に持っているデータを使うだけですし、予測データの計算方法と予め決めた計算方法を最初から最後まで使用します。

重みｗだけが変化し、その結果、予測値と正解値の誤差が変化しますので、誤差を重みｗの関数として表すことができます。これが損失関数(誤差関数)です。

では重みｗをどのように変化させればいいのか、ここが大変重要になってきます。次項から、勾配降下法によって重みを更新する方法を説明します。

重みパラメータwの更新方法

重みパラメータの更新方法はいくつかありますが、その1つが勾配降下法です。勾配降下法を数式を用いずに言葉で説明するなら、勾配が最も急な上り坂を見つけ、それと逆方向に一定距離進むことでパラメータを更新する、ということになります。ここで不明なのは”勾配が最も急な上り坂”はどこかということと、”一定距離”とはどのくらい、という点です。

勾配を調べる(微分)

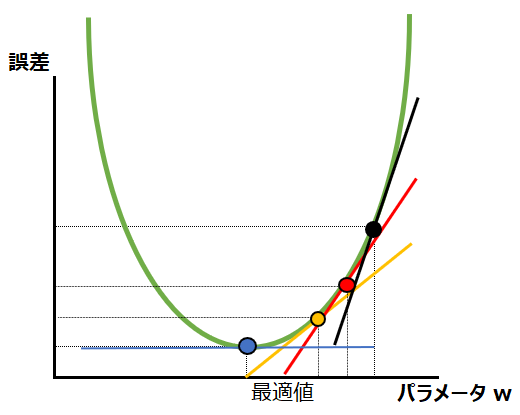
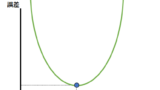
まず勾配が最も急な上り坂は、数学の微分を用いて調べることができます。微分というのは、下記の図で説明するなら、ほんの少しパラメータを変更したときに、誤差がどのくらい変化するかを調べることです。

高校数学で習うように、”ほんの少し”というのを限りなく0に近づけていくと、微分の値はある点における接戦の傾きとなります。この傾きを、上でいう”勾配”と捉えたらわかりやすいかと思います。例えば今、下図の赤い点にいるとしたら、その時点での勾配は赤い接戦の傾きです。そこから右方向に進むと、黒い点のように勾配は急になり、左に進むと黄色い点のように勾配は緩やかになります。最も急な上り坂と反対方向に下ればいいので、この場合であれば左方向に進めばいいことがわかります。

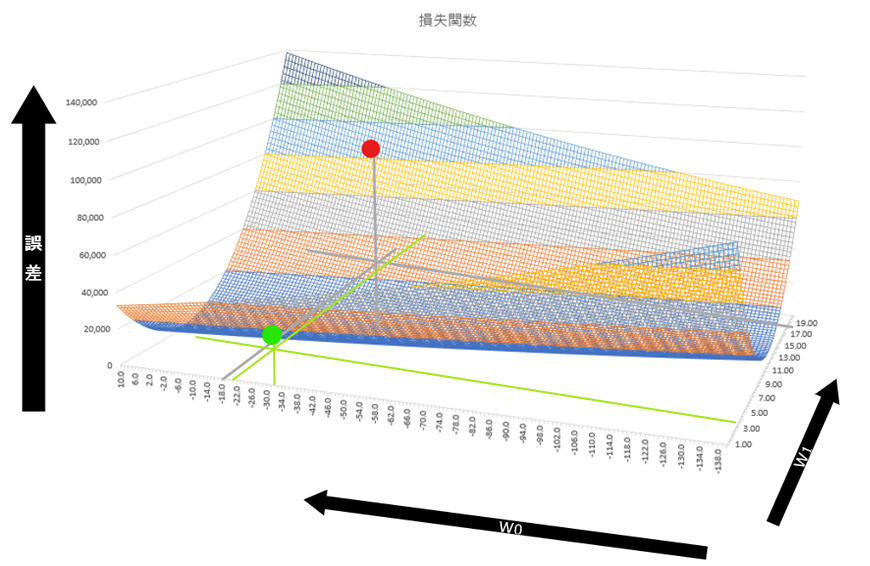
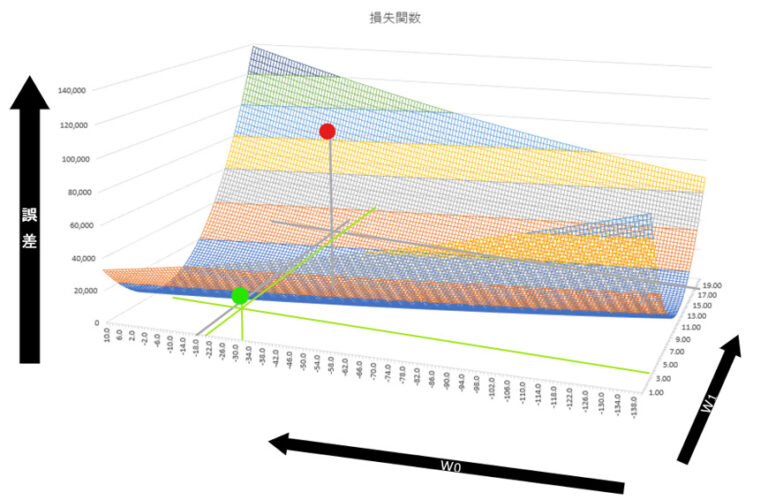
上記は重みパラメータが1つしかない例ですが、パラメータが2つになっても同様に考えることができます。例えば以下は、著者が適当な値で作成したy=w1x+w0(つまりy=ax+b)のタイプの損失関数です。パラメータがw1とｗ0の2つになりました。パラメータという変数2つと、その出力結果の誤差という3つの要素が存在するため、損失関数は3軸になっています。

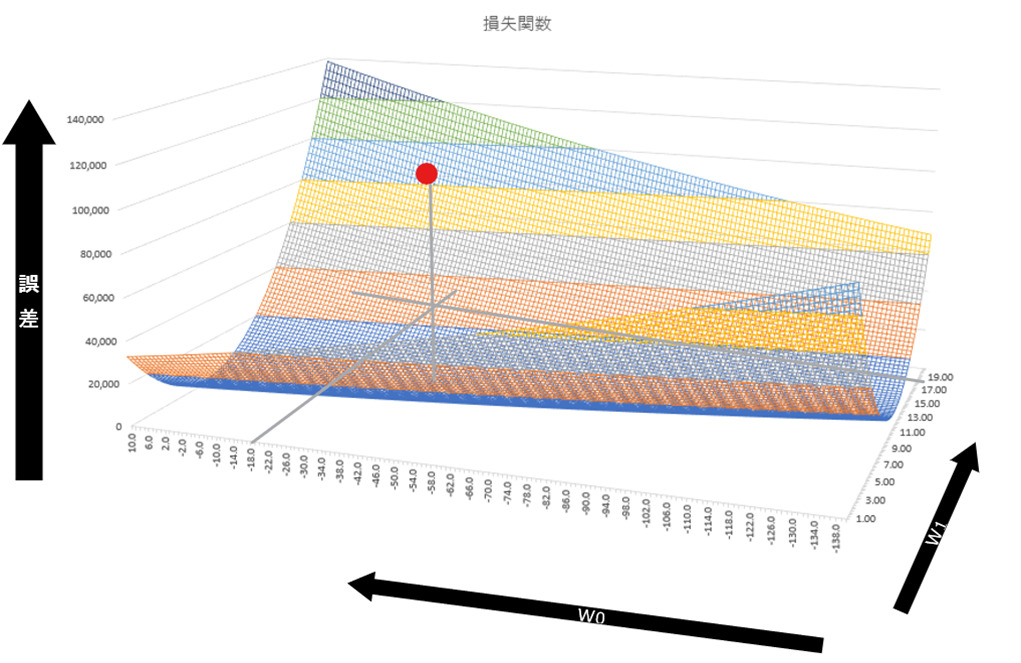
多変数(w0/w1)関数になるので、高校で習う微分ではなく偏微分を用いて勾配を調べます。偏微分は微分と同様、ほんの少しある1つのパラメータを変更したときに、誤差がどのくらい変化するかを調べます。多変数の場合、偏微分した値は接戦ではなく接平面の傾きになります。

上で説明した勾配が最も急な上り坂というのは、言い換えると最も急激に誤差が上昇する方向です。上の図上でｗの初期値が赤い点だった時に、前後(w1)左右(w0)に少しだけ進んだ時に、どの方向が最も急激に上下(誤差)を変化させるかを偏微分によって求め、それとは逆の方向に進むのです。

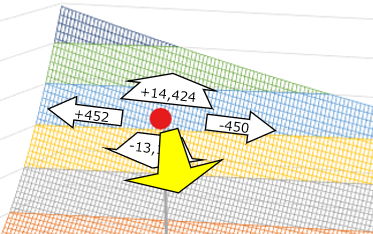
以下の図で、赤い点が(w0,w1)=(-17,18)で、誤差が80,128だとします。この点から前後左右に少しだけ進んだ時(ここではわかりやすく1.0変化した時)に上下(誤差)がどのくらい変化するかを示してみます。

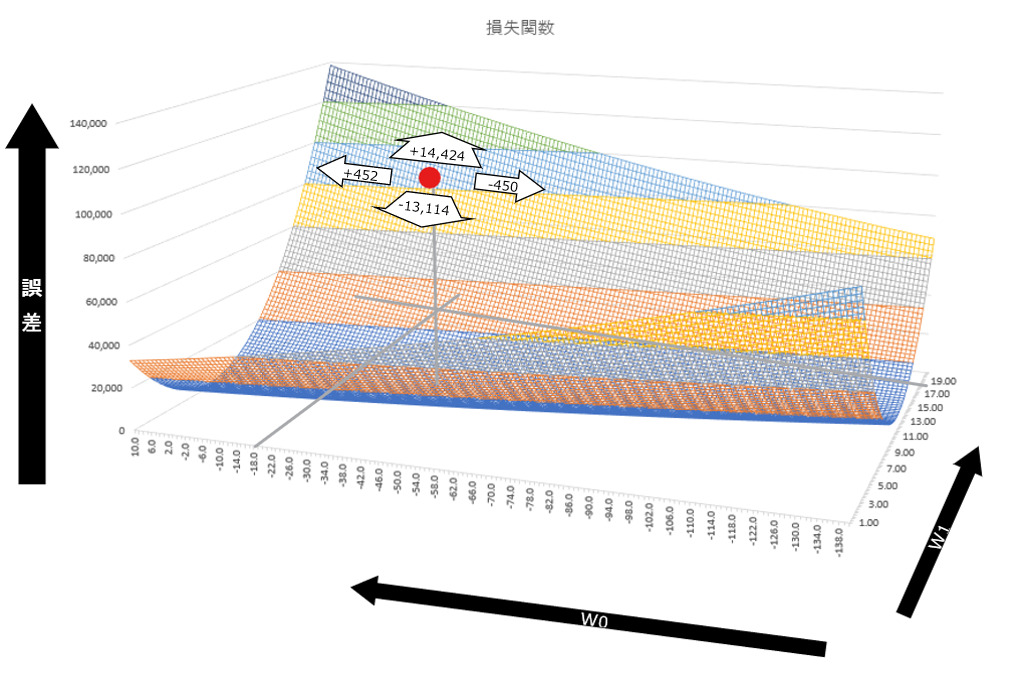
勾配が急なのは、前後方向(w1)では後ろ、つまり奥の方、左右方向(W0)では左であることがわかります。そのため、この例でいえば大きく手前側(w1)かつ少し右側(W0)にパラメータを動かしたら大きく改善されることが直感的にも理解できるかと思います。以下に黄色の矢印で示します。

偏微分の可視化

上の3Dの図で理解しにくい場合には、偏微分の作業を分解して可視化するとよりわかりやすくなります。偏微分というのは、2つ以上ある変数の1つだけを動かして、他を固定した時に、出力がどう変わるかを見る作業です。

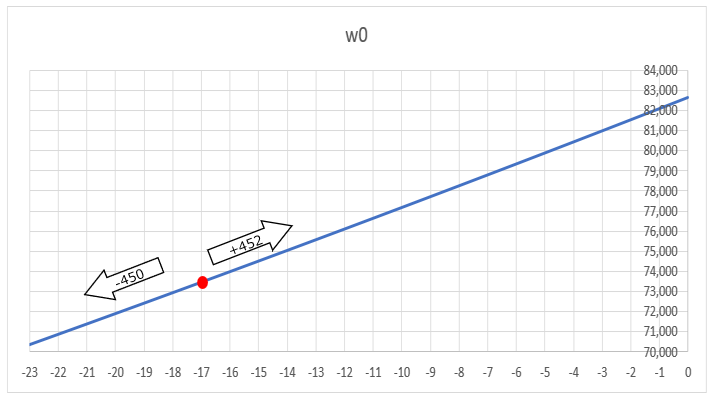
例えば以下のグラフは、w1を初期値の18で固定して、W0だけを変化させた時に誤差がどのように変化するかを表しています。3Dの図で示したように、ｗ0を-17から-16に増やすと誤差は+452、逆に-18に減らすと-450となり、w0を減らす左側に動いた方が誤差が小さくなることがわかります。

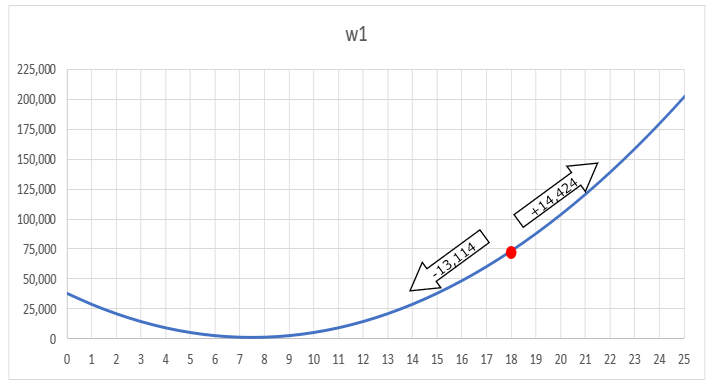
次にw0を初期値の-17で固定して、W1だけを変化させた時に誤差がどのように変化するかを以下で表します。ｗ1を18から19に増やすと誤差は+14,424、逆に17に減らすと-13,114となり、w1を減らす左側に動いた方が誤差が小さくなることがわかります。

学習率を設定する(一定距離)

以上見てきたように、微分を使って勾配を調べることができました。これで、どの方向に一定距離進めばいいかは決定します。次に、一定距離がどのくらいかを決めるために”学習率”を設定します。数式上ではよくギリシャ文字のα(アルファ)やη(イータ)で表記されます。学習率というのは、前項で進む方向を決めるために計算した偏微分の値に適用することで、進む距離に影響を与えます。

例えばここでは学習率を0.001としてみます。上の図で、勾配が急なのは前後方向(w1)では後ろ側の+14,424、左右方向(W0)では左の+452であることを示しました。上述の通り、勾配降下法では最も急な勾配と逆方向に一定距離進みます。この一定距離を以下のように計算してみましょう。

上で学習率を0.001と設定しました。まずw1ですが、急勾配の変化量は+14,424です。これに0.001をかけると14.424です。さらにこれをマイナスにすることで、w1の更新料は-14.424と求められます。上で赤い点のw1は18としたので、w1の更新後の値は 18.000-14.424＝3.576となります。

同様にW0の更新は、- (0.001 x 452) = -0.452 となります。赤い点のw0は-17としたので、w0の更新後の値は-17 – 0.452＝-17.452 になります。

上の計算からもわかる通り、学習率を大きな値に設定すれば1回の更新でｗを大きく動かすことができることがメリットで、反対に学習率を小さな値に設定すると、ｗを細かく調整できることがメリットになります。