機械学習のモデル構築を進めるうえで最も重要なポイントの一つが、いかにして最適なパラメータ(w)を見つけるか、ということです。今回は、その為の手法の1つである正則化について説明します。
正則化とは何か
正則化(regularization)というのは、適切な係数を取捨選択したり、係数の大きさを小さくすることによって過学習を防ぐ手法です。過学習については以下の記事を参照ください。
別の言い方をすれば、関係のなさそうな係数を捨てたり、係数の大きさを調整したりして、本当に重要な係数を見つけるようなイメージです。
係数が少なくなれば、モデルもより単純になります。5次関数・6次関数のような高次関数によるぐにゃぐにゃした無秩序なグラフよりも1次関数や2次関数の方が使えそう、、というのは直感的にも理解できるものかと思います。
正則化には後述するように様々な手法がありますので、精度がなかなか高くならない時はいろいろ試してみて、精度がより良くなるように目指しましょう。
なお、似た名前の正規化については、正則化とは全く異なりますので、注意してください。正規化については以下の記事を参照ください。
損失関数 + 正則化項
正則化では、損失関数にモデルの複雑さを示す正則化項を加えます。損失関数の記事では、平均二乗誤差について数式を使わずに説明をしましたが、今回は数式を全く使わないのは難しいので、以下の通り、平均二乗誤差の式を使います。

意味としては1番目からN番目までのデータについて、予測値(yp)と正解値(yt)の誤差を2乗した値をすべて足したもの(∑)を、データ数で割る(1/N)ことで平均を出しています。この平均二乗誤差が小さくなるように、重みパラメータwを設定するのが機械学習です。詳細は以下の記事を参照ください。
この損失関数に、以下のように正則化項λR(w)を加えることで、正則化を実現します。
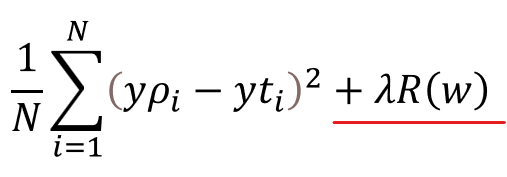
正則化項
正則化項λR(w)は、パラメータのλ(ラムダ)と、ノルムのR(w)部分に分かれます。それぞれ、意味を以下で説明します。
パラメータλ
損失関数に対してノルムをどのくらい反映させるかを決めるパラメータです。勾配降下法における学習率と同じようなイメージを持ってもらえるとわかりやすいでしょう。λを大きく設定すれば正則化項による損失関数の調整効果が大きくなり、λを小さくすればその逆となります。実際には、学習の進み具合を見ながらλを調整していきます。
なお、勾配降下法については以下の記事を参照ください。
ノルムR(w)
上項でR(w)と記したノルム(Norm)というのは、ベクトルの大きさの指標です。まずはそのイメージを掴んでみましょう。例えば重みパラメータが3つ存在する予測モデルを作るとして、今その重みが以下のように設定されているとします。
- w0= 1
- w1= 5
- w2= 3
これをベクトルとして捉えると以下のように図示することができます。

数学的に表現すると、1,5,3という成分を有する3次元ベクトルです。このベクトルの大きさについて以下のようにL1ノルム、L2ノルムのような方法で大きさを測ります。
重みパラメータの値が大きい=ベクトルが大きいとノルムR(w)も大きくなり、それが以下の損失関数において誤差を悪化させる要因になります。逆に言えば、重みパラメータの値が小さいほど、損失関数を改善することになります。

これをより直感的に理解するために、y=w0 + w1x1 +w2x2といった表される線形回帰モデルの重みについて考えてみましょう。
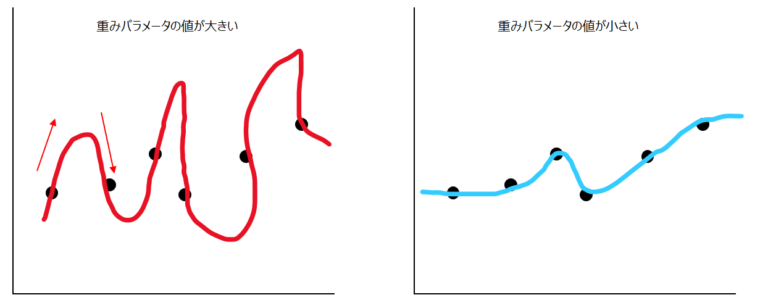
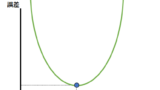
重みパラメータ(w0, w1, w2)の値が大きいと、以下の赤いグラフのように、線の傾きも大きくなります。結果的に、関数もより複雑になり、汎化性能(学習だけでなく汎用的に使える性能)が落ちてしまいます。
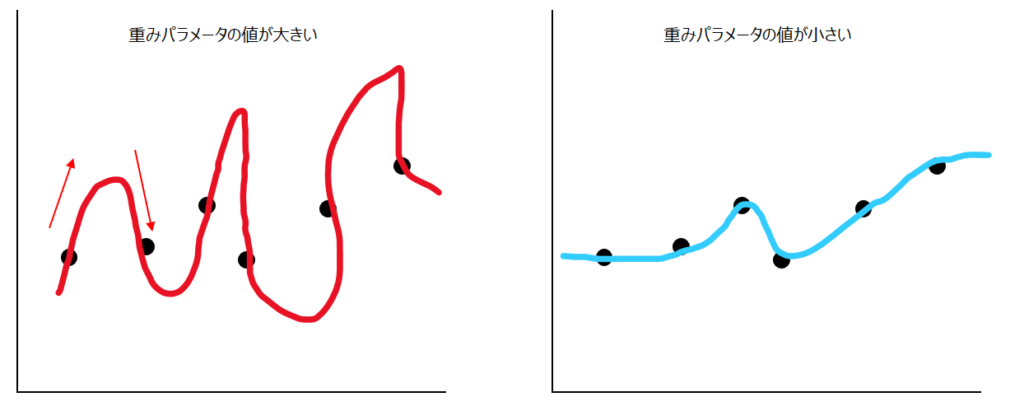
一方青いグラフは、赤いグラフと同じようにアップダウンは繰り返していますが、より汎用性が高まっていることが直感的にわかると思います。正則化項にノルムR(w)があることで、赤いグラフよりも青いグラフの方が高評価されるようになるのです。
これがノルムR(w)を正則化項に加える意味になります。それを踏まえて、具体的にL1ノルムとL2ノルムについて説明します。
L1ノルム
L1ノルムは、以下の通り、重みパラメータwの絶対値を合計します。
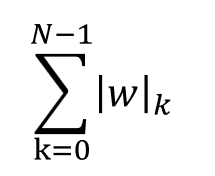
上で例示したようにw0=1、w1=5、w2=3という3つの重みがあるという前提で説明します。lwlの外側の線は”絶対値”という意味ですので、lwlkというのはwkの絶対値という意味です。∑によって、kは0から重みの数であるNから1を引いた数までを合計します。重みがw0, w1, w2の3個であれば、N=3、w0, w1, w2の絶対値の合計、という意味です。上のケースでは、1+5+3でノルムは9になります。
L2ノルム
L2ノルムは、以下の通り、重みパラメータの2乗値を合計して平方根を取ります。
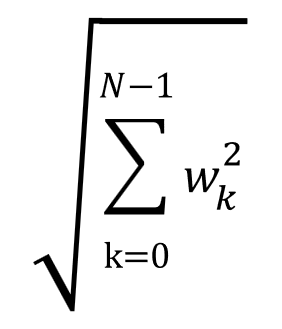
w0=1、w1=5、w2=3であれば、2乗和である1+25+9=35の平方根となり、√35、約5.9になります。
Lasso回帰とRidge回帰
上述のL1ノルムやL2ノルムを正則化項に加える具多的な手法が、Lasso回帰やRidge回帰と呼ばれる手法です。L1ノルムを使った正則化、つまりL1正則化を行うのがLasso回帰で、L2正則化を行うのがRidge回帰です。
Lasso回帰はL1ノルムを使っているため、重みパラメータの値が0の値である時に損失関数の値が小さくなります。重みパラメータの値が0ということは、その重みが掛かっている説明変数も0になります。
このことから、Lasso回帰は結果的にたくさんある説明変数を選択する役割を果たします。多すぎる説明変数を削減したい時に有用です。このように重みパラメータの値で0が多くなる性質のことを”疎”の英語表記を用いて”スパース性”と呼びます。
一方のRidge回帰はLasso回帰ほど重みパラメータを0にする作用はありませんので、説明変数の数は減らしたくないが、重みを調整することでなだらかで汎用性の高い予測モデルを生成したい時に有用です。
ユークリッド距離とマンハッタン距離との関連
ではなぜ、L1正則化にはスパース性があるのでしょうか。これを数学的に理解するには数式を大量に使う必要があり、それは著者の方向性と反してしまうため、ここでは直感的な理解を助けてくれるであろう、ユークリッド距離とマンハッタン距離の違いを説明します。
それぞれ、L1ノルムはマンハッタン距離、L2ノルムはユークリッド距離と関連付けて説明します。我々が日常使う”距離”という概念は、数学的には非退化性、対称性、三角不等式という3つの距離の公理を満たす概念であると明確に定義されています。ユークリッド距離とマンハッタン距離はその距離の公理を満たす距離の測定方法の具体例です。
ユークリッド距離とマンハッタン距離を説明するために、以下のような2軸上の2点の距離をどのように図るかを想定しましょう。以下の図を、(x, y)平面で理解してください。

ユークリッド距離
我々が数学の授業で習うのはユークリッド距離の方です。ユークリッド距離は以下のように計算できます。
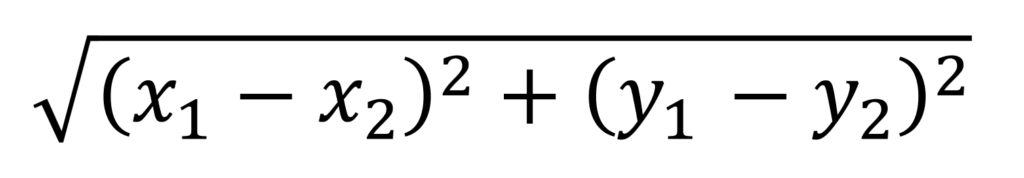
もしこれだけ見てピンとこなければ、以下のピタゴラスの定理を思い出してください。2点間の距離を、直角三角形に見立てると、求めたいのは斜辺の長さに該当します。
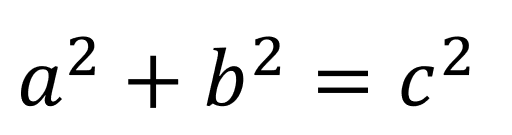
計算すると、2点間の距離は5√2であることがわかります。√を外すと約7です。

このユークリッド距離の考え方だと、同じ距離は同心円状に広がります。以下の円の上であれば、どこも地点Aからの距離は変わらず、約7です。
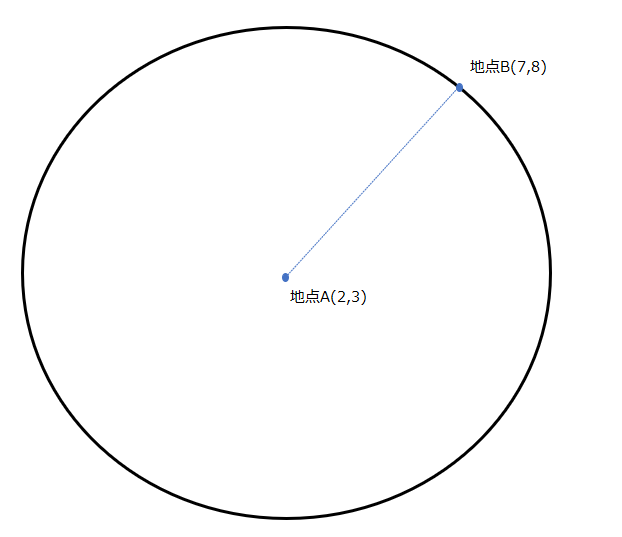
2乗して求めることからもわかる通り、ユークリッド距離というのはL2ノルムに該当します。以下のユークリッド距離の計算式とL2ノルムの計算式を再度眺めてもらえれば想像できる通り、これらは同じことをしています。各軸方向(各重みパラメータ)の値を2乗して平方根を取ることで、ノルム(ベクトルの大きさ)を算出しています。

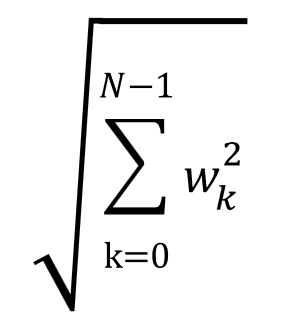
マンハッタン距離
続いてマンハッタン距離について説明します。マンハッタン距離は以下のように計算されます。
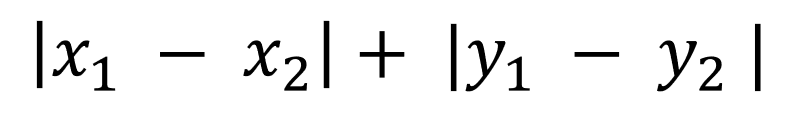
見慣れていないとイメージがしにくいかもしれませんが、全く難しくなく、我々が日常使う”みちのり”の概念と同じだと考えてください。ユークリッド距離は2点を直線で結んだ時の距離を求めましたが、以下のように地点A・Bを移動するのに縦方向と横方向にしか進めないようなケースであれば、マンハッタン距離で計算する方が実際に即しています。
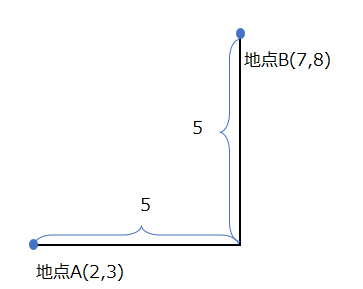
マンハッタン距離で計算すると、5+5=10が2点間の距離になります。実際、マンハッタン距離という名前は、ニューヨークのマンハッタンが日本の京都と同じように碁盤の目のように縦横に整備された街並みをしていることに由来します。
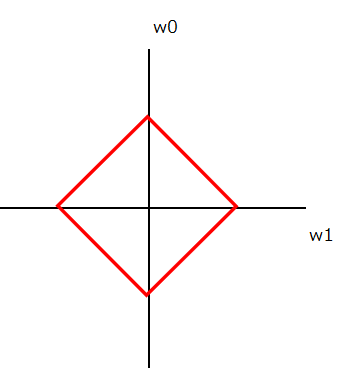
ユークリッド距離では同じ距離は同心円状に広がりましたが、マンハッタン距離では以下の赤枠のように、菱形上に同じ距離が広がります。
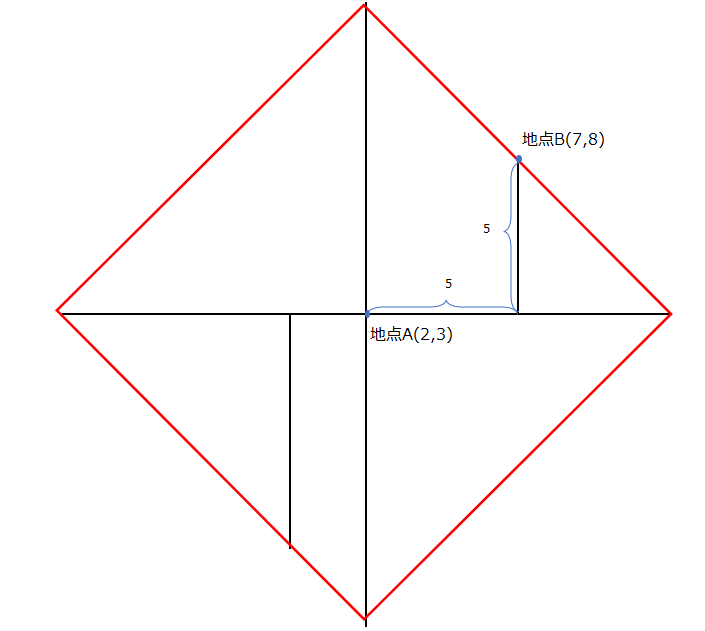
絶対値を取ることからもわかる通り、マンハッタン距離というのはL1ノルムに該当します。以下のマンハッタン距離の計算式とL1ノルムの計算式を再度眺めてもらえれば想像できる通り、これらは同じことをしています。各軸方向(各重みパラメータ)の絶対値を取ることで、ノルム(ベクトルの大きさ)を算出しています。
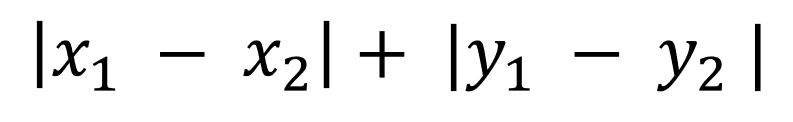

L1正則化のスパース性
マンハッタン距離の説明の中で、マンハッタン距離=L1ノルムは同じ距離(同じ値)が菱形上に広がると説明しました。これがL1正則化のスパース性につながります。
上では2点間の距離で説明しましたが、それを重みパラメータにすり替えてみましょう。以下のようにパラメータがw0/w1の2つしかないことを想定してください。赤い菱形はL1ノルムの大きさ、つまりマンハッタン距離が同じであるため、L1正則化であるLasso回帰の正則化項において、赤い菱形上の点は全て損失関数に同じ影響を与えます。言い換えると、モデルの良し悪しに影響する評価が同じということです。
菱形が45度傾いていることからもわかる通り、L1ノルムの方は、w0もしくはw1どちらかが0になるようなエリアが多く存在します。(以下、左図の青部分)
一方、L1(菱形)とL2(円形)を重ねるとわかる通り、L2の方がw0もw1も0以外の何らかの値を取るエリアが広いことがわかります。(以下、右図の黄色部分)
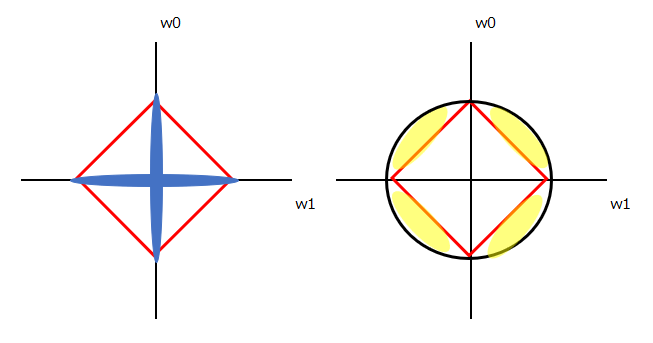
言い換えると、L2ノルムよりL1ノルムの方が、各重みパラメータ(上ではw0もしくはw1)が0になるような状態を高く評価するような計算式になっていると言えます。
ことほどさように、L1ノルムを用いるLasso回帰の方が、重みパラメータの値で0が多くなる性質であるスパース性が高いのです。
変数選択
上ではRidge回帰やLasso回帰のような、損失関数に正則化項を追加する方法を説明しました。これらは正則化の中でも縮小推定と総称されています。本項目では、正則化の中の変数選択という手法を簡単に紹介します。
変数選択は、係数の取捨選択をする正則化の種類です。特に係数を一つずつ選んでON/OFFを切り替えながら各係数の影響を見ていく漸次的選択法が使われることが多いです。
前向き漸次的選択法
初めにすべての係数をOFFにして、そこから1つずつ係数をONにしながら、精度の向上を目指す方法です。
後ろ向き漸次的選択法
初めにすべての係数をONにして、そこから1つずつ係数をOFFにしながら、精度の向上を目指す方法です。


コメント