私たちが日常よく耳にする”陽性” とか”陽性” という精度に関する言葉、皆さんはどういう意味なのか説明できますか?精度というのはある測定や検査がどのくらいの正確さで実施されているかを表す言葉ですが、以下に説明するように様々な概念や使い方や意味があります。
今回は、新型コロナウィルスの万円以降よくメディアで聞くようになったPCR検査を例に、”精度”について解説します。
個別の検査結果の精度を表す指標
今回はPCR検査を例に説明しますので、まずは個別の検査結果の精度を表す指標を説明します。
陽性と陰性
まずは、陽性(Positive)と陰性(Negative)について。この言葉はコロナ以降、PCR検査の結果を表す言葉として頻繁に使われるようになりました。意味は以下の通りです。
陽性(Positive)
ある検査で反応が現れることです。
陰性(Negative)
ある検査で反応が現れないことです。
偽陽性と偽陰性とは何か
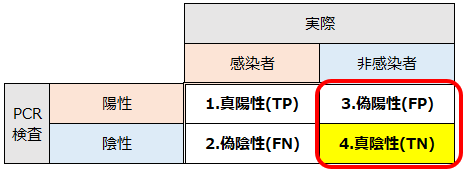
陽性と陰性以外にも、偽陽性・偽陰性という言葉も耳にするかと思います。こちらはどういった意味なのか、同じくPCR検査を例に、以下の混合配列と呼ばれる図を使って説明します。

1.真陽性(TP:True Positive)
感染している人が、検査の結果も陽性である場合を真陽性と呼びます。
2.偽陰性(FN:False Negative)
感染している人が、検査の結果は陰性である場合を偽陰性と呼びます。
3.偽陽性(FP:False Positive)
感染していない人が、検査の結果は陽性である場合を偽陽性と呼びます。
4.真陰性(TP:True Positive)
感染していない人が、検査の結果も陰性である場合を真陰性と呼びます。
検査結果全体の精度を表す指標
上述のように、陽性・陰性という概念を使って個別の検査の結果の精度を確かめることができます。では、複数の検査結果の全体の精度はどのように確認すればよいかを説明します。
感度と特異度
まずは、感度と特異度について説明します。
感度(真陽性率)
感染者の中で、検査結果も陽性であった人の割合のことです。以下の赤枠の中の黄色部分に該当し、真陽性率とも呼びます。ここが最も検出したい場所であり、そこをどのくらいの”感度”で検知できているか、という指標であると言えます。

特異度(真陰性率)
非感染者の中で、検査結果も陰性であった人の割合のことです。以下の赤枠の中の黄色部分に該当し、真陰性率とも呼びます。
全体の精度を測る4つの指標
次に、検査全体の精度を測るための4つの指標を紹介します。ここでは概念についてだけ簡単に説明し、後述のケーススタディにて具体的に数字をあてはめながら説明します。
正解率(accuracy)
正解率は全データに対する、実態と検査結果が一致している割合です。一般的な”精度”のイメージに最も近いのではないでしょうか。計算式は以下の通りです。Nは検査数全体の数だと理解してください。

以下の赤枠の中の黄色部分に該当します。

適合率(precision)
適合率は、陽性反応全体の内、実際に感染している割合です。計算式は以下の通りです。
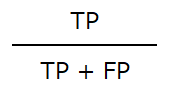
以下の赤枠の中の黄色部分に該当します。

再現率(recall)
再現率は、感染者全体の内、陽性検出できた割合です。計算式は以下の通りで、上述の真陽性率と同じ結果になります。

以下の赤枠の中の黄色部分に該当します。

F値(F score)
F値というのは、適合率と再現率の調和平均です。後述するように、適合率と再現率はデータによって大きく乖離することがあります。F値はそれら2つの調和平均を取ることで、適合率と再現率どちらかだけで判断すると偏った結果になってしまう際に参照できる値です。計算式は以下の通りです。

調和平均
なお調和平均というのは、比や割合を平均したい時に用いる計算方法で、通常我々が用いる算術平均ではうまく平均値を算出できない際に使われます。以下の図を用いて簡単に説明します。
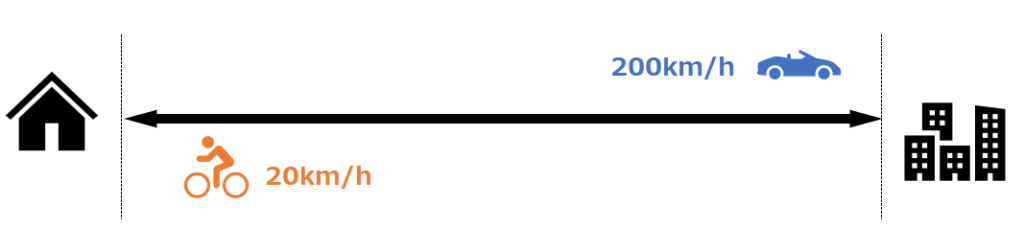
自宅から外出先まで、行きは車を使って時速200km、帰りは自転車で時速20kmで帰宅したとします。この時の平均時速は、算術平均では(100+20)/2 =110km/hとなります。これ、何かおかしいと思いませんか?例えば行き先が100km先だったと仮定すると、時速110kmであれば往復で2時間かからないはずです。
しかし行きと帰りの実際の所要時間は行きに30分、帰りに5時間かかり、合計で5時間半となります。200kmに5時間半かかるということは、速度は約36kmになるはずです。これは、速度という概念がみちのり/時間という”割合”で示される概念であり、算術平均では正しく計算できないことによる齟齬です。
そこで使われるのが調和平均です。割合同士を平均するときには調和平均を用い、データの合計数をそれぞれのデータの逆数を足した値で割ることで平均を算出します。今回のケースでは、データの数は200と20で”2″。逆数というのは、200であれば1/200、20であれば1/20です。それらを考慮し、以下の計算式によって、今回のケースでの調和平均を求めることができます。

ケーススタディ
ではここから、全体の精度を測る指標を用いて、感染者100人・非感染者9,900人を含む合計1万人を対象にPCR検査をした仮想のデータを使ってケーススタディをします。それぞれ、感度(真陽性率)と特異度(真陰性率)に任意の数字を設定し、正解率・適合率・再現率・F値がどのような値になるかを見ていきましょう。直感的なイメージを得るための参考にしてください。
ケース①【感度99% 特異度97%】
陽性者をより正確に検知できるように、まずは感度99%、特異度97%を想定します。
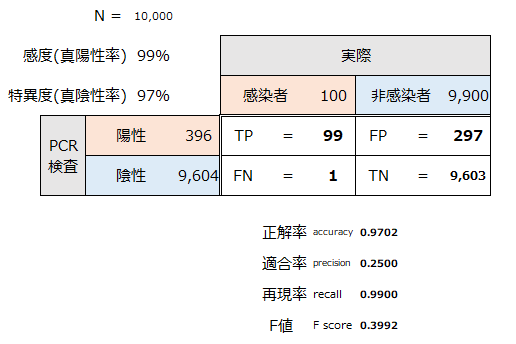
正解値
TPとTNを分子に取る正解率は、そもそも非感染者の数が感染者よりもかなり多いため、TNに引っ張られて特異度の97%に近い数値が出ています。
適合率
陽性(TPとFP)を分母に取る適合率は、数の多い非感染者に影響されて、25%と非常に低い数値が出ています。
再現率
再現率は上で見た通り、感度と一致して99%です。
F値
F値は適合率と再現率の調和平均を取り、約40%です。
ケース②【感度97% 特異度99%】
続いて偽陰性をできるだけ少なくするように、感度97%、特異度99%を想定します。
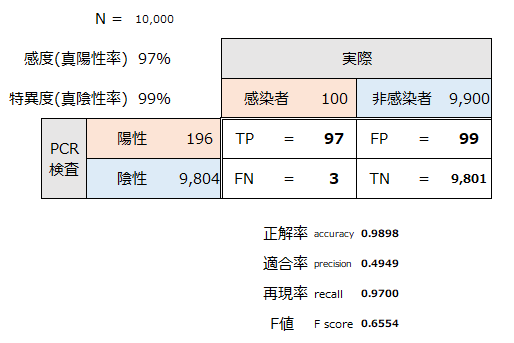
正解値
TPとTNを分子に取る正解率は、ケース①と比較して更にTNが大きく増加したため、正解値もTNに引っ張られてケース①よりも改善して特異度に近い約99%が出ています。
適合率
陽性(TPとFP)を分母に取る適合率も、偽陽性のFPの数が減少したためケース①より大きく改善し、49%となっています。
再現率
一方感度と一致する再現率は悪化し、97%です。
F値
F値は適合率と再現率の調和平均を取り、約66%です。



コメント