最小二乗法の記事でも述べたように、機械学習において最も重要なポイントの一つが、いかにして最適なパラメータ(w)を見つけるか、ということです。今回は最適なパラメータを設定するために理解が不可欠な損失関数(=誤差関数)について説明します。最小二乗法については以下の記事を参照ください。
損失関数(誤差関数)
損失関数というのは、予測値と正解値の誤差についての関数です。機械学習では、モデルの精度を誤差で評価します。直感的に理解できると思いますが、予測値と正解値の誤差は小さければ小さいほどよいので、誤差が最小になる様にモデルを設計します。損失関数を理解するために、まずは機械学習がどのようなプロセスで行われるかを見てみましょう。
機械学習の流れ
プロセス図
機械学習のプロセスは、単純化すれば以下の通りです。
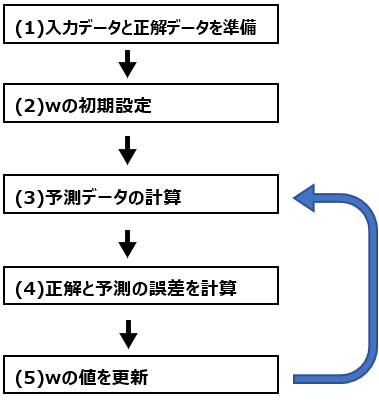
(1)入力データと出力データは、例えば気温とその日のアイスクリーム販売量データです。気温が入力データ、アイスクリーム販売量が出力データになります。
(2)その後、重みパラメータwの初期設定を行います。とりあえず全て1にすることもあれば、ランダムに値を設定することもあります。
この先は規定回数繰り返します。
(3)まずはwの値と入力データを掛け算した値を元に予測データを計算します。ここでより細かくどのように計算するかが、いわゆる”機械学習のアルゴリズム”です。線形回帰とロジスティック回帰ではwと入力データの掛け算した値に対する計算方法が異なります。
(4)初めに正解データも用意しているので、ここで予測データと正解データがどのくらい合っているかを確認します。気温が30度の時のアイスクリーム販売量が300個と予想したのに、実際は320個だったら、20個の差があります。後述のMSEという方法で誤差を計算すると、この誤差は400になります。このように、誤差というのは具体的な値で計算されます。
(5)誤差が大きければ、wの値が適切ではないことになるので、wの値を変更します。これを重みパラメータの更新と呼び、機械学習における1つのキーポイントになります。
wを更新したら、更新後の値を使って再度(3)から繰り返します。
重みwと誤差の関係
機械学習のプロセスからもわかる通り、機械学習における変数は重みパラメータwだけです。入力データと正解データは既に持っているデータを使うだけですし、予測データの計算方法と予め決めた計算方法を最初から最後まで使用します。
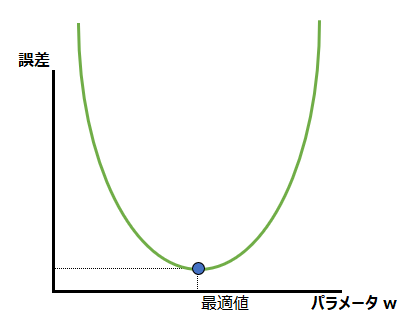
重みwだけが変化し、その結果、予測値と正解値の誤差が変化しますので、誤差を重みwの関数として表すことができます。詳しくは後述しますが、それが損失関数であり、以下のようなグラフで表現されるものになります。
損失関数(誤差関数)とは何か
上述の機械学習のプロセスを前提に、損失関数とは何かについて説明します。
誤差とは何か
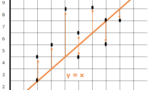
まずは、誤差についてもう少し詳しく説明します。前項の機械学習のプロセスで述べたように、誤差とは予測値と正解値の差のことです。ではそもそも予測値と正解値の誤差とは何か、という点から説明します。前回の最小二乗法の記事中でも出てきた以下の図を再度見てみます。

この図中の点は、実際のデータでした。それに対してオレンジの太線( y = x )は、これらデータ群を説明するために引いた直線です。この時、予測値というのはオレンジの太線、正解値というのは実際のでーたあである黒い点です。その誤差というのはオレンジの太線から出ているオレンジの細い矢印です。
前回の最小二乗法の話の復習にもなりますが、この誤差が小さいほど、予測値であるオレンジの太線は確からしい、別の言い方をすれば精度が高いと言うことができます。
平均二乗誤差(MSE)
誤差の代表例はMSEです。最小二乗法の記事でも説明した通り、上述の誤差を二乗して合計(残差平方和)したり、その平均を取る(平均二乗誤差, MSE)ことで、モデルによる予測と実際のデータの正解がどのくらい近いか、モデルの精度がどのくらい高いかを数値化することができます。再掲になりますが、上図の残差平方和と平均二乗誤差は以下の通りです。
y=x : 誤差(0,4,4,1,1,16,4,0,4,1)
残差平方和:35
MSE:3.5
このMSEは、回帰問題で頻用されます。
交差エントロピー誤差(CE)
回帰問題の損失関数としては上述の平均二乗誤差(MSE)がよく使われますが、分類問題に対しては交差エントロピー誤差(CE:Cross Entropy)が使われます。
交差エントロピー誤差については別記事で説明しますので、そちらを参照ください。
損失関数の特徴と勾配降下法
回帰問題の誤差を表すMSEと分類問題の誤差を表すCEに共通するのは、誤差がプラスの値を取り、パラメータの値に応じて誤差の値が変化し、どこかに最適値が存在するということです。そのような誤差とパラメータの関数が損失関数(誤差関数)であり、それをグラフにすると、例えば以下の図のようになります。横軸にモデルの重さパラメータwがあり、その値によって縦軸のMSEやCEのような誤差が決まる、という関数になっています。
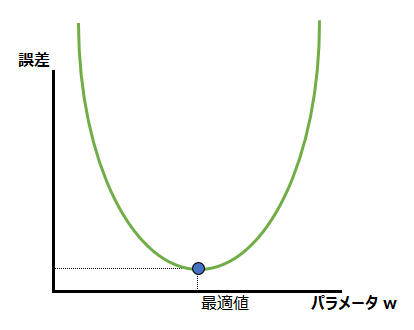
最適なパラメータが設定されれば、MSEは0もしくは最小値になります。完璧なモデルを作ることができればMSEは0になりますが、現実には難しいので、MSEが最小になることを目指します。図上で、最適に設定されたパラメータは右に動かし過ぎても、左に動かし過ぎてもMSEが悪化してしまいます。
では、どのように最適なパラメータを設定できるのか。それを探す方法の1つが勾配降下法です。勾配降下法については、以下の記事を参照ください。

コメント