今回はRNNの一種であるLSTM(Long Short-Term Memory)について解説します。RNNについては以下の記事を参照ください。
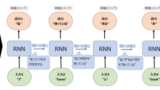
LSTMとは何か
LSTM(Long Short-Term Memory)は文章・音声・時系列のようなシーケンシャルなデータの長期的な依存関係を扱うように設計されています。その名の通り、長期記憶と短期記憶両方を保持するような構造を実現しています。
LSTMは1997年の論文で発表されました。LSTMの背後にある考え方は、従来のRNNが逐次データの長期的な依存関係を処理する際の限界に対処することでした。LSTMの主な貢献は、メモリセル、ゲートを導入し、長期間にわたって情報を保存できるようにしたことです。
LSTMを理解するための前準備
長期記憶と短期記憶
RNNの記事で紹介した通り、隠れ状態hはある時間ステップまでにネットワークが処理した情報をまとめたベクトルです。直感的に説明するなら、”過去の入力全体に対する理解”と言えます。しかし、同じ記事で説明した通り入力が長くなると昔の記憶を保持できなくなります。これは、人間の短期記憶に似ています。
LSTMではこの隠れ状態hを短期記憶として使いつつ、別に長期記憶cというものを用意して、その両方を保持することで長い文章の処理などを可能にします。なお、cはcontext(文脈)の頭文字です。
ゲート
LSTMのもう1つの大きな特徴は、ネットワークの隠れ状態における情報の流れを制御するゲートという機構を持つことです。ここでいうLSTMのゲート機構は、Forget Gate、Input GateとOutput Gateの3つで構成されています。
ゲートの役割は、RNNの前の時間ステップからの情報の流れを調整することです。情報の流れを調整するとは、前の時間ステップから次の時間ステップに渡される情報の量と種類を制御することです。
より具体的には、0から1の値を出力するSigmoid関数を用いて、どの情報が重要かを判断します。Sigmoid関数は、現在の入力(x)と前の隠れ状態(h)を入力として、次に渡すべき情報は1に近い値、捨てるべき情報は0に近い値を生成します(そうなるように、以下の重みwを学習する)。この値が大きいほどより多くの情報を渡すべき、小さいほど情報を渡すべきでないとすることで、情報を制御しているのです。このように0~1で情報量を制御する機構を一般にゲート機構と呼びます。
BPTTの問題
Backpropagation Through Time (BPTT) は、Recurrent Neural Networks (RNN) を学習するために用いられる学習アルゴリズムです。BPTTは勾配降下法を用いて重みを更新する際に、誤差逆伝播法(Backpropagation)のように層を逆から辿るのではなく、時間ステップを逆から辿ります。勾配降下法・誤差逆伝播法については以下の記事を参照ください。
BPTTは誤差逆伝播法と同じように、勾配が消失する問題を抱えていました。これは、RNNの学習において誤差を時間的に逆伝播すると、重みに対する誤差の勾配が非常に小さくなり、ネットワークが長期的な依存関係を学習することが困難になるというものです。例えば長文を入力すると、前半の意味や記憶を保持することが非常に難しくなります。
LSTMでは上述の長期記憶と短期記憶を両方保持することで、この勾配消失問題にも対処しています。
LSTMの構造
具体的には後述しますが、以下はLSTMの全体像です。以下では、隠れ状態hについては、イメージがしやすいように”記憶”や”理解”といった言葉も用いて説明します。
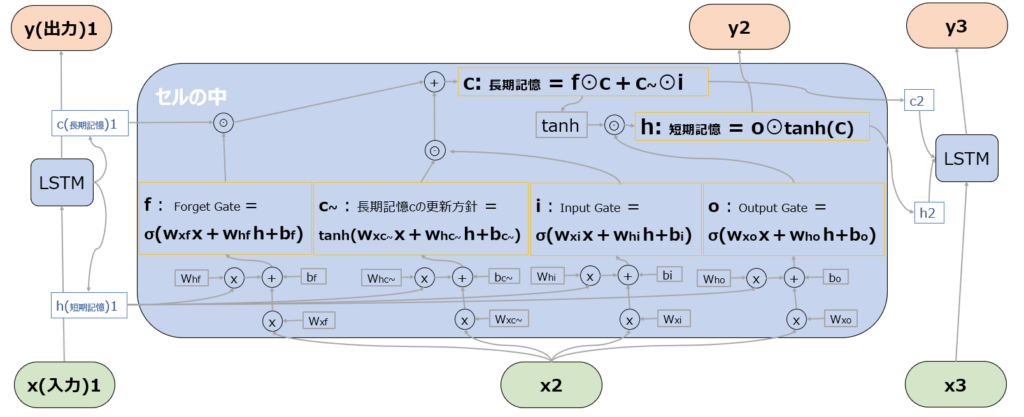
また下記ではSigmoid関数やtanh関数という活性化関数が登場します。活性化関数については以下の記事を参照ください。
Forget Gate
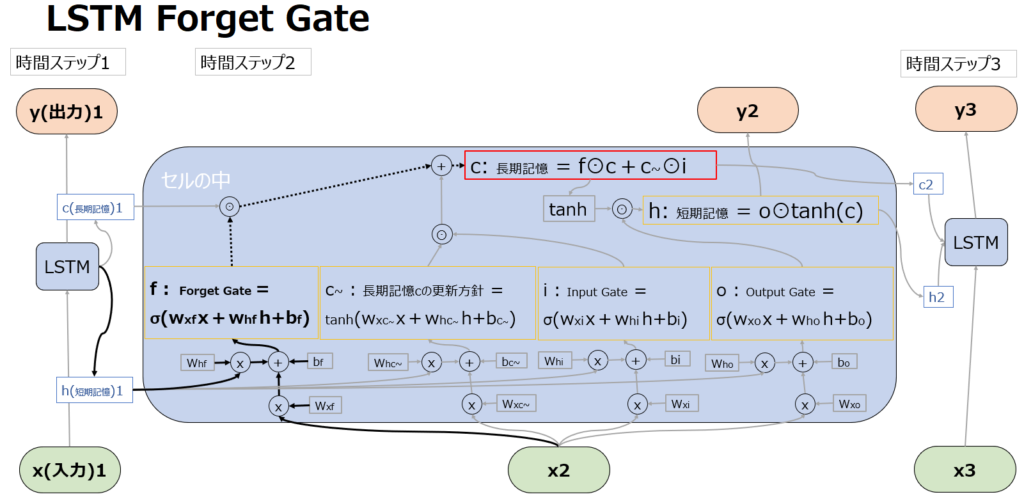
Forget Gate を計算するSigmoid関数(σ)は、現在の入力(x2)と以前の短期記憶(h1)を入力とし、長期記憶を忘却する”Forget”の度合いを表す値を生成します。ここで計算された値が、長期記憶cの更新時に、直前の長期記憶c1と掛け合わされます(点線部の先の赤枠)。⊙はアダマール積と呼ばれる処理で、行列の成分同士の積です。
Sigmoid関数の性質によりForget Gateの計算結果は0~1の値を取ることからわかる通り、長期記憶を維持したい場合はここが1となるように、長期記憶を大きく書き換えたい場合はここが0になるように学習されます。
直感的な理解のために例を出すと、例えば文章に冠詞の”a”が出てきたとしても、それは長期記憶のすべての意味ベクトルにおいて影響しないため全てSigmoid関数が”1″と出力されるように学習されるかもしれないが、”Unfortunately”という単語が出てきたら、意味ベクトルのうち “Positive / Negative” や “Happy / Sad” などのベクトルでは長期記憶を書き換える必要があるかもしれず、一部Sigmoid関数が”0″と出力されるように学習されるかもしれない、といったイメージです。
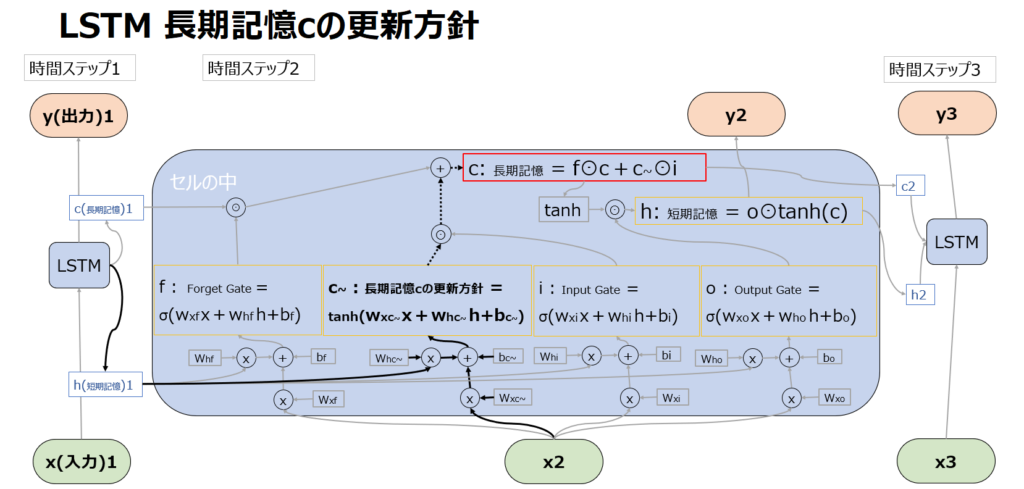
長期記憶cの更新方針(c~) =g
LSTMにおいては、tanh関数を使った処理も出てきます。これはfやiやoのようにxやhをどのくらい次に渡すかを調整しているわけではないのでゲートではないですが、Input Gateの出力iをどのくらい長期記憶に追加するかを決めています。
具体的には以下の図の点線部の先の赤枠内の通り、c~をiとかけた(⊙はアダマール積)値を、Forget Gateの出力を受けて忘却を経た長期記憶cに足し合わせることで、長期記憶を強化しています。
Input Gate
Input Gate を計算するSigmoid関数(σ)は、現在の入力(x2)と以前の短期記憶(h1)を入力とし、長期記憶を強化する”Input”の度合いを表す値を生成します。詳細はc~の項で説明した通り、ここで計算された値が長期記憶cの更新時に、c~と掛け合わされて長期記憶を強化しています。

長期記憶cの更新 -CEC
既にf,c~,iの項目で説明した通りですが、以下の2つの合計値で長期記憶を調整しています。
f⊙c:過去の長期記憶の一部又は全部を忘却
c~⊙i:新しい記憶の一部又は全部を追加

ちなみにこの長期記憶の機構のことをCEC(Constant Error Carousel)と呼びます。名前の由来は、上述の勾配消失問題と関連します。入力が長くなるとBPTTにより誤差逆伝播した際に勾配消失を起こしやすくなりますが、CECではf⊙cとc~⊙iを加算しています。掛け算で層を深くすると逆伝播の微分値がどんどん0に近づいて行って勾配消失が発生しますが、足し算の場合は勾配が1になります。CECの値は逆伝播されてもエラーを一定に保てるということが、Constant Errorの意味で、Carouselはぐるぐる回る遊具のことですが、RNNも系列に沿ってぐるぐる回るので、CECと呼ばれるのです。
Output Gate
Output Gate を計算するSigmoid関数(σ)は、現在の入力(x2)と以前の短期記憶(h1)を入力とし、LSTMの出力であるyと短期記憶であるhを計算するのに使われます。yという出力値に対する調整機能を持つことから”Output” Gateという名前になっています。
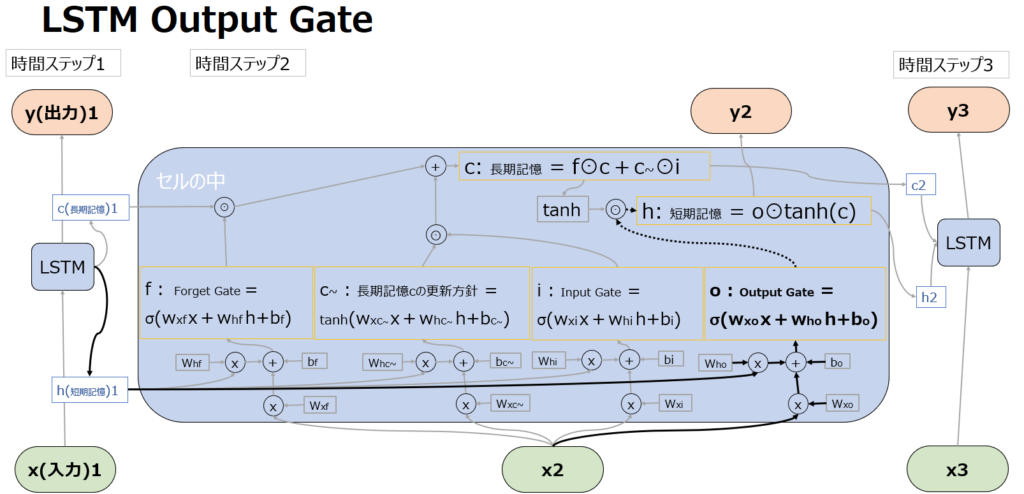
出力yと短期記憶(隠れ状態)hの出力
既に計算されているcとoを使って、yとhを出力します。
長期記憶はf⊙c(過去の長期記憶の一部又は全部の忘却)とc~⊙i(新しい記憶の一部又は全部の追加)を足したものですが、これをtanh関数に通すことで、-1~1の範囲に値を変換することができ、扱いやすくなります。
そのtanh(c)に対して、oは長期記憶のcは使わずxとhという短期の情報だけを用いて出力されていますので、oとtanh(c)を掛け合わせる(⊙はアダマール積)ことで、長期記憶の中から短期に必要な情報を抽出しています。

以上が、LSTMの説明でした。




コメント