【強化学習】ベルマン方程式を日本語に翻訳すると？

今回は、強化学習に触れると必ず出てくるベルマン方程式について、数式の意味をできるだけ言語で解説してみます。

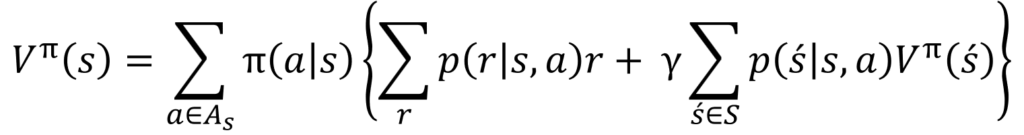
過去の記事については以下を参照ください。

なぜベルマン“方程式“なのか？
ベルマン方程式を日本語訳する

なぜベルマン“方程式“なのか？

“方程式”とは、数学において二つの式が等しいことを示すもので、等号（=）を使って表されます。方程式の目的は、未知の値（変数）を求めることです。たとえば、x+2=5 という簡単な方程式では、x が何であるかを求めることになります。解は x=3 です。またy=２x +1のような2変数の場合であれば、yかxどちらの値がわかれば、もう一方(未知数)もわかります。これが方程式です。

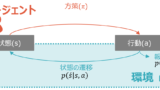
この文脈で言うと、ベルマン方程式では、何がわかれば何がわかる、と言っているのでしょうか。詳細は後の章を見てもらえればと思いますが、今の状態で取り得るすべての行動aと、その行動によって移行する次の状態 s′の価値 V(s′)がわかれば、今の状態の価値V(s)がわかる、と言っているのです。

ベルマン方程式を日本語訳する

ではいよいよ、冒頭のおっかない数式を解読してみましょう。まずは状態価値関数V(s)のベルマン方程式です。

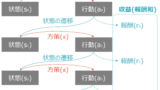
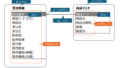
以下のように、部品ごとに色を分け、部品の意味を日本語で説明してみました。

しかし、これではまだ直感的にイメージできないので、各部品を野球で喩えてみます。

s=攻撃側8回裏1アウト1,3塁、1点差ビハインド。

π=各方策(犠牲フライ狙い、シングルヒット狙い、HR狙い、スクイズトライ、内野ゴロ狙い、四球狙いなど)をそれぞれ採用する確率(=確率分布)

a=πに従って選択される。(最も確率の高いものを選ぶか、もしくはそこにランダム性が加わる)。選択肢の数は方策の数分ある。

p(r|s,a):各aを実行した時に報酬をもらえる確率(=作戦が成功する確率)

r:作戦が成功した時の報酬。仮に報酬＝野球の得点とするなら、犠牲フライ狙い、シングルヒット狙い、スクイズトライ、内野ゴロ狙いの場合はr=1。HR狙いならr=3。四球狙いならr=0(ただしs'以降にプラス影響)

割引率：ハイパーパラメータ。今の打者で得点を取りたい場合はこれを低めに設定、最終的に得点できればいい場合は高めに設定する。

s'=πの選択肢数、およびaの選択肢数だけs'も存在しうる(一部重複しうる)

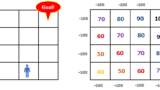
s'の状態価値=上の項目と同様、a',πなどを使って計算できる。

これら野球で例えば部品を、上のベルマン方程式に代入すれば、計算ができます。つまり、ベルマン方程式からわかるのは、ありえる全ての選択肢を考えていけば、V(s)を計算できる、つまり今の状態を定量的に評価できるということです。

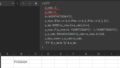
同様に、状態行動価値関数Q(s,a)のベルマン方程式も日本語訳してみました。