過去の記事で、勾配降下法では大域的最適解に辿り着けない問題があることを紹介しました。前回記事は以下から参照ください。
今回は、勾配降下法の問題を解決するための手法であるOptimizer(最適化関数)について、SGD、Momentum、AdaGrad、RMSProp、Adamを例に解説します。
SGD(確率的勾配降下法)
SGDについては以下の記事で説明していますのでご参照ください。参考まで、SGDは1960年代に登場しました。
SGDの数式は以下のように表すことができます。
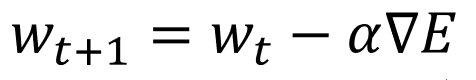
見慣れていないと非常にわかりにくいと思いますので、まずは以下の通り意味を付け加えます。

こうすると、過去の記事で解説した通り、勾配降下法が、損失関数の勾配が最も急な上り坂(∇E)を見つけ、それと逆方向(-)に一定距離(学習率α)進むことでパラメータを更新するアルゴリズムであることが数式でも確認できると思います。当該記事は以下を参照ください。
過去の記事では何とか数式を使わずに説明しましたが、今回はOptimizerそれぞれを解説するのに数式が不可避です。まずは上記のSGDの数式を基に、後述のMomentum、AdaGrad、RMSProp、Adamがどのような工夫を凝らしているかを直感的に理解していきます。
Momentum
1980年代に登場したMomentumの数式は以下の通りです。
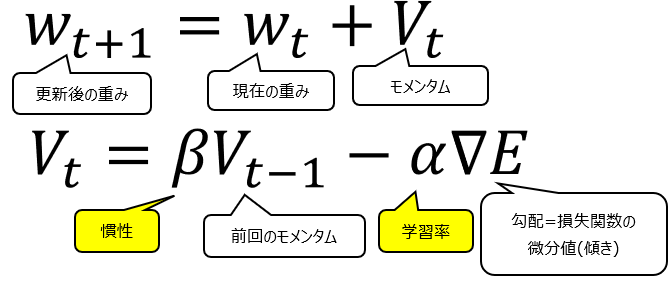
Momentum(勢い、運動量)という言葉の通り、慣性が働くような設計になっています。一見すると赤線部のようにSGDはマイナスに対しモメンタムはプラスの計算をしていて真逆のように思えますが、
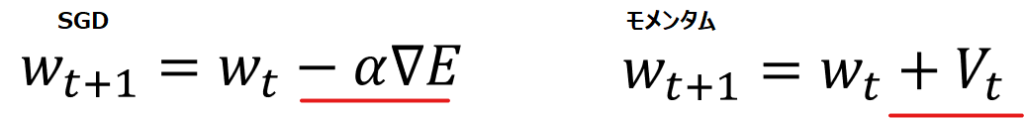
以下青線部のように、実際はVの中身に”-α∇E”が含まれますので、この部分はSGDと全く同じであることがわかり、黄色背景の部分がMomentumの特徴であることが同時に見て取れます。
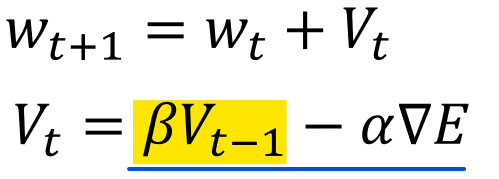
では黄色部分は何を計算しているかと言うと、自分で設定するハイパーパラメータであるβ(慣性)を使って、1回前のwの更新量(vt-1)をどのくらい反映するか、という内容になっています。
ここでβが大きいと、慣性が強い、つまり前回の更新量の影響を強く受けるということです。高速道路で自動車を運転している際に急ブレーキをかけても車体が前へ進み続ける、まさに慣性のイメージと一致しますね。一方βを0にすると、慣性が0となりSGDと同じ数式になることがわかると思います。
以下は架空のデータを使って重みwの更新をSGDとMomentumで比較した様子です。慣性をβ=0.2と設定したところ、特に2回目・3回目の更新のところでMomentumはSGDより大きく更新していることがわかります。

上記のようにMomentumは、パラメータ更新する際に前回のパラメータ更新量の一定率を加算することで、ジグザグではなく慣性を持つような動き、加速して下るような動きを見せます。
AdaGrad
2011年に登場したAdaGradの数式は以下の通りです。
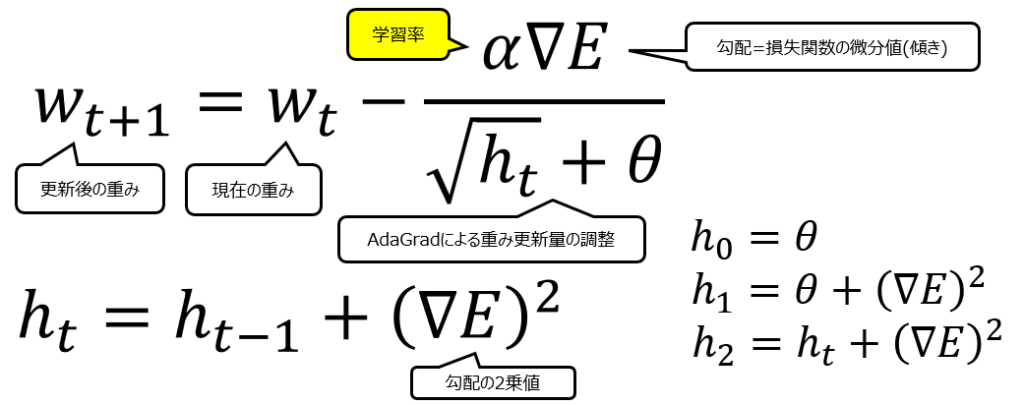
SGDとAdaGradでメインの式を比べてみると、違いは赤枠部分の更新量が、黄色部分の√ht+θで割り算されていることです。θはハイパーパラメータで一定の値なので、本質的には√htによって更新料を調整しているのがAdaGradであると言えます。
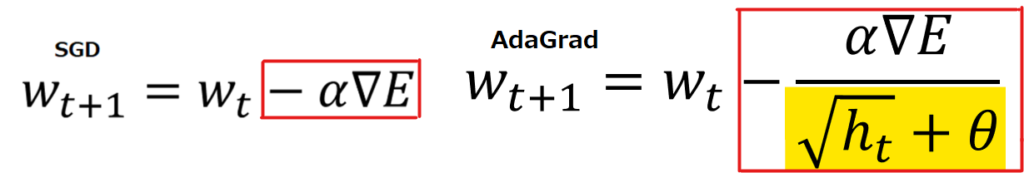
ではhtはどのように計算されているかというと、計算式は以下の通りです。

初回のh0はハイパーパラメータθをそのまま使います。2回目のh1では、前回のhであるθ+その時点でのwの勾配の2乗値。ここからがポイントで、3回目のh2ではh1+その時点でのwの勾配の2乗値です。h1には前回の時点でのwの勾配の2乗値が入っているわけですから、勾配の2乗値が3回目以降どんどん蓄積されていくことになります。
htに過去の勾配の2乗値が蓄積されていくということは、wの更新式の分母√htの値もどんどん大きくなることが想像できると思います。

以上を纏めると、AdaGradはパラメータ更新の際に過去のパラメータ更新量の情報をすべて使うことで、最初は大きくパラメータを更新して、徐々に更新量を減衰させていることが特徴として挙げられます。
RMSProp
RMSPropはAdaGradの改良版として2012年に発表されました。RMSPropの数式は以下の通りです。
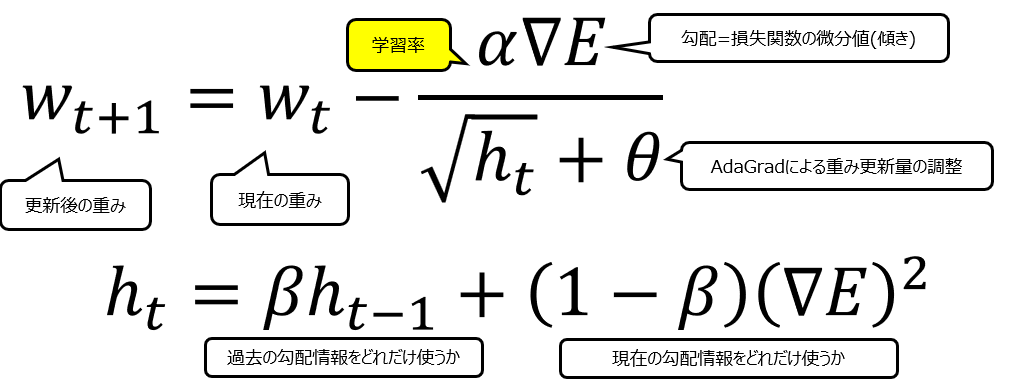
メインのwの式はAdaGradと全く同じです。異なるのはhtの式で、βというハイパーパラメータを新たに設定することで、過去の勾配情報をどの程度用いて更新するかを設定することができ、それによってAdaGradでは実現しないジグザグの動きを可能にします。以下は、AdaGradとRMSPropのhtの式の違いと、それによるwの動きの違いを説明する図です。

まず先の項目で説明した通り、AdaGradのht(水色)は過去の勾配を蓄積していくので常に値が大きくなり、√htがw更新式の分母になる為wの更新量は常に小さくなります。結果として左のグラフのように、wの更新は滑らかに、少しずつ平坦になっていきます。
一方のRMSPropは、過去の勾配をそのまま蓄積しません。緑色のβht-1の部分で過去の勾配を使いますが、ハイパーパラメータβが掛け合わされることでその影響が弱まります(βを大きくするとAdaGradと似た動きをします)。そして黄色部分の現在の勾配はその時々で値の大小は異なるので、その合計である水色のhtも、値の大小がバラバラになり、これがグラフでジグザグの動きとして現れます。
纏めると、RMSPropはAdagradと同様に学習率を調整しますが、Adagradを改良してβという新たなパラメータを設定することで、学習率を減衰させることもできるし、ジグザグの動きも可能にしています。これによって現在の勾配が大きい時には大きく更新できる余地を残すことができました。
Adam
Adamは2015年に導入されました。MomentumとRMSPropのアイデアを組み合わせています。収束が早く、さまざまな問題でうまく機能し、現在最もよく使われているOptimizerの1つです。Adamの数式は以下の通りです。
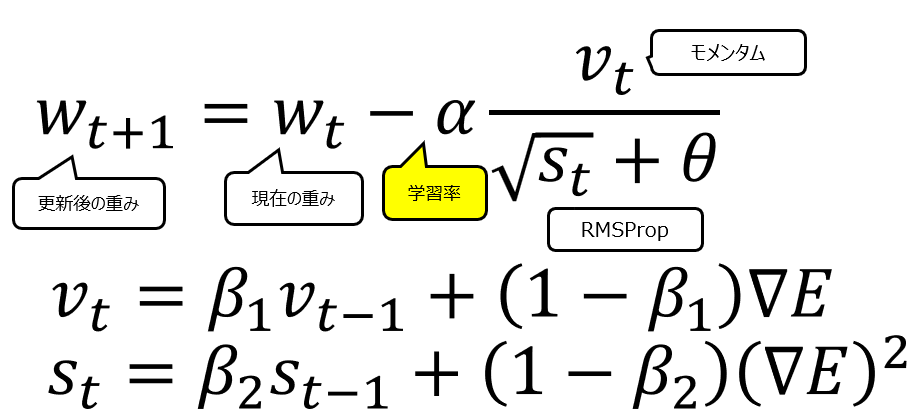
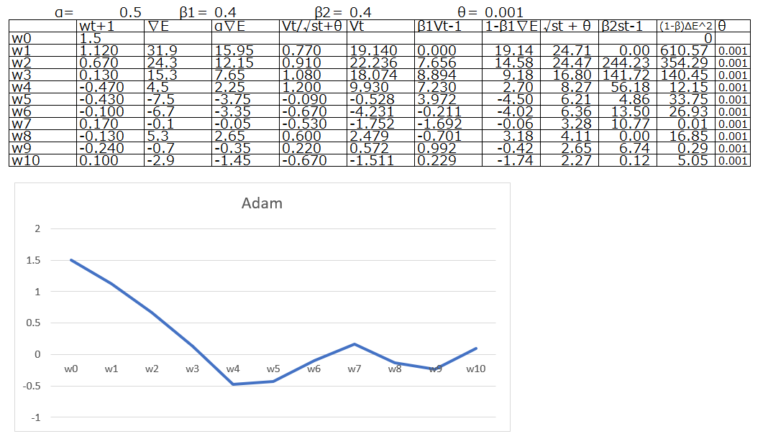
数式を見てもらえればわかる通り、メインのwの更新式の学習率αの後続部分で、分子にモメンタム、分母にRMSPropを置いています。結果として以下のグラフの通り、より複雑な動きが可能になっています。
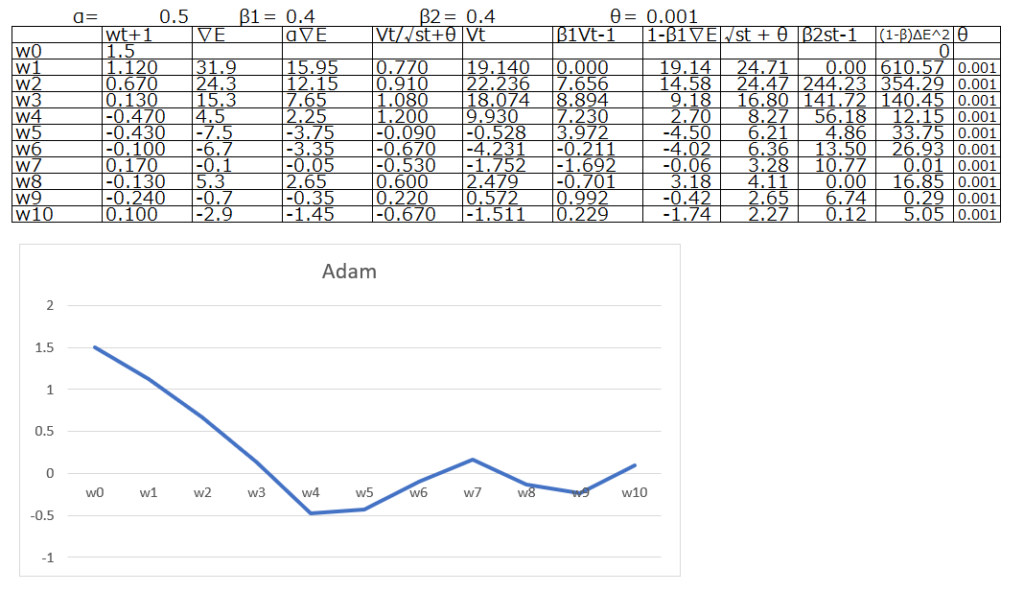
纏めると、RMSpropとMomentumの要素を融合したのがAdamです。非常に安定していて、現時点でOptimizerとして非常に頻繁に使用されます。何を使えばいいのか迷った場合には、まずはAdamで学習率にデフォルト値を設定して使用されることが多いです。
なお、これらoptimizerの動きについて更に深く理解したい場合は、以下の動画がおすすめです。
Deep Learning精度向上テクニック:様々な最適化手法 #1



コメント