今回は機械学習の中の教師あり学習の分野における、ロジスティック回帰について解説します。機械学習の概要や基本的な用語の説明については以下の記事を参照ください。
ロジスティック回帰とは何か
ロジスティック回帰というのは、分類問題における確率を予測する統計手法です。分類問題には2値分類と多値分類がありますが、ロジスティック回帰は通常は2値分類に適用されます。2値分類というのは答えが2つの分類問題です。病気の有無、死亡と生存、合格と不合格のように、2つの分類で分けることのできる分類を扱います。
名前の由来
ロジスティック回帰の名前の由来については諸説ありますが、ロジスティック関数(方程式)と今回登場するシグモイド関数の類似性から命名された可能性があります。”ロジスティック”というのがわかりにくいので、”シグモイド回帰”と呼ばれることもあります。
また、”回帰“という言葉が入っていることから混乱しやすいですが、回帰問題ではなく分類問題を扱うので、注意してください。ではなぜ”回帰”と呼ぶのかというと、最終出力値こそ”0/1″のような離散値(例:病の有無)ですが、その前段階ではシグモイド関数を使って連続値である確率値(病気の可能性XX%)を出力しており、その点では線形回帰と似たような処理と言えるのです(非線形回帰と言える)。線形回帰については以下から参照ください。
ロジスティック回帰による予測
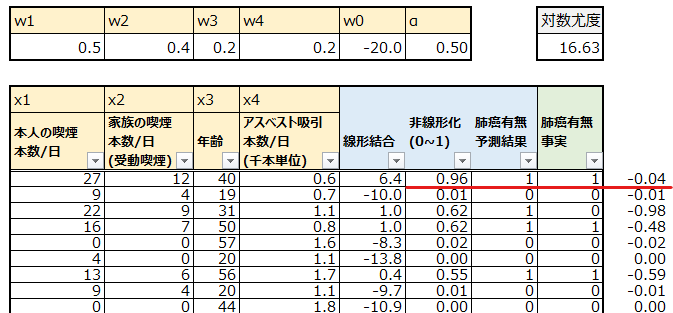
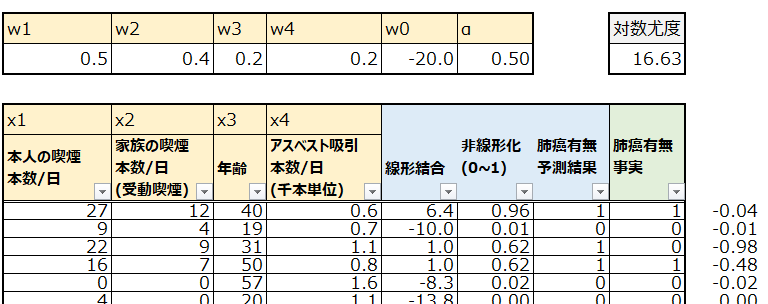
今回は以下の架空のデータを使います。75人分の肺癌に関するデータです。ベージュ部分、肺癌に関係しそうな説明変数として、本人の喫煙、受動喫煙、年齢、アスベスト吸引という4つを用意しました。青色部分はロジスティック回帰の予測プロセスで使います。緑色は実際に肺癌かどうかで、肺癌の場合は1、そうでない場合は0です。
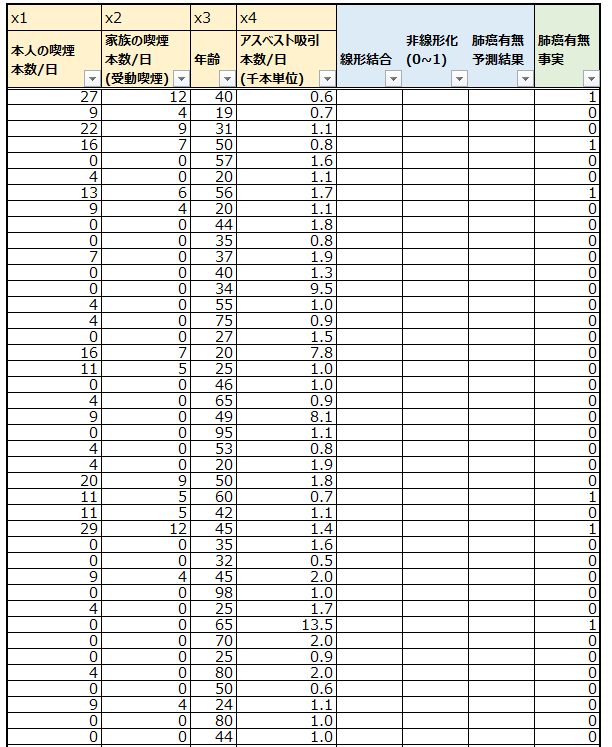
重み付き線形和の計算
まずは線形回帰と同様に、各説明変数についての重みwとバイアス項を用意し、入力された説明変数との重み付き線形和を計算し、複数の説明変数から予測のための1つの指標を得ることができました。なお、wはまずはそれっぽい適当な値を投入しています。
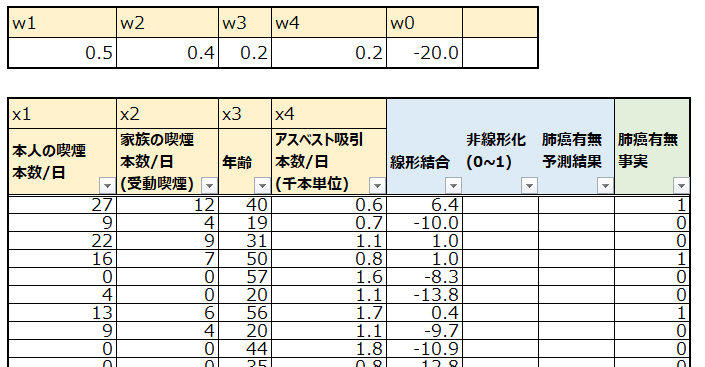
ここで線形和は、以下のように計算されています。
w1x1 + w2x2 + w3x3 + w4x4 + w0
例えば一番上の人の線形和の計算は以下のようになっています。
0.5*27 + 0.4*12 + 0.2*40 + 0.2*0.6 -20 = 6.42
シグモイド関数による非線形化
続いて線形和の値にシグモイド関数を適用して非線形化し、予測値の元となる値を出力します。
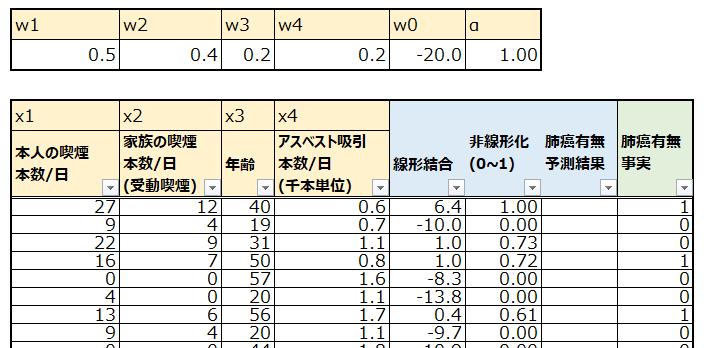
計算方法は以下の通りです。

αは値が0に近いほど曲線が滑らかになり、大きいほどステップ関数に近くなります。

シグモイド関数については以下の記事も参照ください。
2値で予測
最後に、シグモイド関数の出力値0~1から、肺癌有無を予測します。今回は閾値を0.5に設定し、0.5以上の場合は1(肺癌有り)、未満なら0(肺癌なし)とします。

これで、一通りの予測が完了しました。
ロジスティック回帰の精度
上記にて、ロジスティック回帰による予測を一通り完了しましたが、果たしてこの予測はどれほど正しいのでしょうか。
この予測の正しさを評価するために、ロジスティック回帰では対数尤度が使われます。対数尤度は以下のように計算されますが、これだけだと意味がよく分からないので、具体的に見ていきます。
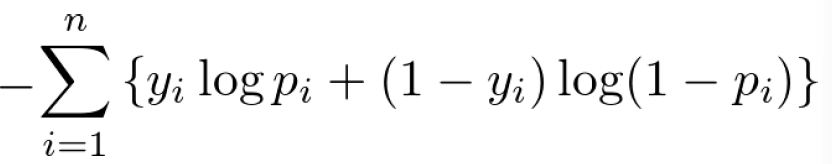
先ほどの表の欄外でそれぞれの対数尤度を計算し、表の右上で合計してマイナスしています。まず1人目ですが、対数尤度は-0.04となっています。この意味は何でしょうか?
先ほどの計算式を日本語訳すると以下のようになります。
-Σ(事実肺癌有無)*log(非線形化の値) + (1-事実肺癌有無)*log(1-非線形化の値)
1人目の計算の内容は以下の通りです。
1*log(0.96) + 0*log(1-0.96) = -0.0408
この計算を解釈していきます。まずlogは本質ではないので、まずlogを取ります。
1*(0.96) +(1-1)*(1-0.96)
その上で、まず前半部分です。
1*(0.96)=0.96
これは、“1”という肺癌の事実と、0.96という肺癌有の確率を掛け合わせています。この値が大きいほど、高確率で1(肺癌有り)と予測できていて、かつそれが正解していると言えそうですね。
次に後半部分です。こちらは0で掛け算されているので、0になりますね。
(1-1)*(1-0.96) = 0*(0.04)=0
2人目の計算も見てみましょう。
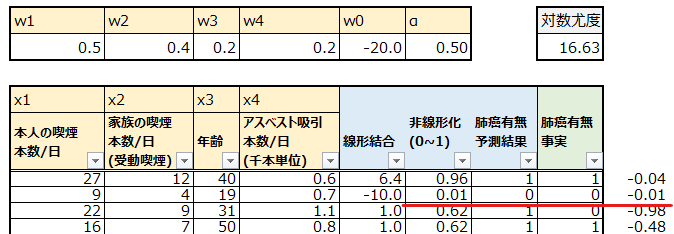
logを取った計算内容は以下の通りです。
0*(0.01) +(1-0)*(1-0.01)
今度は後半部分で、どれだけ自信を持って0と予測したかを反映することができています。
(1-0)*(1-0.01)=0.99
続いて3人目です。今度は様子が違いますね。そもそも予測を外しています。

logを取った計算内容は以下の通りです。
0*(0.62) +(1-0)*(1-0.62)
前半部分が0になるので、後半部分が重要です。以下のようになっています。
(1-0)*(1-0.62)=0.38
前の2人と比べて、正解の方の選択肢の確率が38%(間違った選択肢の確立が62%の為)しかなかったということで、計算結果も小さな値となっています。
ここまで3人の結果をまとめると以下のようになります。
- 1人目:0.96
- 2人目:0.99
- 3人目:0.38
ここで初めて、尤度とは何か、なぜlogをつけ、なぜマイナスが付いているかを説明します。
尤度と同時確率
まず尤度(Likelyhood)は”もっともらしさ“です。尤度という概念が使われるのは、正しい”確率”が事前にわかっていないケースです。
例えばコイン投げにおいて、事前に表と裏が出る確率が0.5ずつだとわかっている場合、その前提で得られたデータの起きる確率を計算することができます。例えば5回コインを投げて4回表が出る確率は以下のように計算できます。
5C4 * 0.54 * (1-0.5)(5-4) = 0.1565
つまり、表と裏が出る確率が0.5ずつだと予めわかっている場合に5回コインを投げて4回表が出る確率は15%だということです。まあまあ珍しい現象だということですね。これが我々が学校で習う通常の確率の考え方であり、このように複数の事象(5回コインを投げて4回表)が同時に起きる確率のことを同時確率と呼びます。
なお上記の計算方法がわからない場合は下記の二項分布の項目を参照ください。
それに対し”尤度“を考えるときは、事前に正しい確率がわかっていません。あくまでわかっているのは手元のデータで、そこから、元々の確立を考えます。
元々数学に強い方は、関数の書き方の方が理解しやすいかもしれません。以下の通り、通常の同時確率f(x|p)は”確率p(50%)がわかった上で、手元のデータがxの場合”の確率を出力しますが、尤度の場合はL(p|x)”手元のデータがxの場合に、確率pがXX%である”ことがどれほど尤もらしいかを出力します(p=20%はそれほど尤もらしくなく、p=50%はそこそこ尤もらしく、p=80%が最も尤もらしい、など)。

ではロジスティック回帰のケースでどのように尤度を計算しているのかを説明します。今回は、まず適当にwを設定しました。それを前提に、”もしwがこの値だった時、肺癌の確率がpである尤もらしさ“が尤度です。確率はそれぞれの事象が独立の時は掛け算することができるので、上から3人目までの尤度は以下のように計算できます。
L = 0.96*0.99*0.38=0.36
このように、シグモイド関数の出力値を掛け算することで、尤度、つまり重みをあるwに設定した時の肺癌の予測確率p(0.96等)がどれほど尤もらしいか(それっぽいか)を計算することができるのです。
二項分布
二項分布(Binomial distribution)というのは、ベルヌーイ試行が成功する成功する回数の確率分布です。ベルヌーイ試行というのは、1/0、表/裏、当たり/外れのように2通りの結果しか出ないような試行のことです。
二項分布の確率は以下のように計算できます。nは試行回数(何回コインを投げたか)、kは事象の回数(表が出た回数)、Pは事象の確率(表の確率)です。
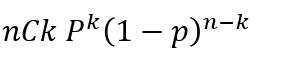
対数尤度
尤度については説明しました。ではなぜlog(対数)を取るのか。これは単に計算上の都合です。上述の様に確率pを何度も掛け算すると、その結果はどんどん小さい値になっていきます。パソコンというのはあまりにも小さな値の場合、うまく扱えなくなったり、人間が意図したのと違う数値を返してしまいます。
そのため、便宜的に尤度のlogを取ります。logを取ると、元々0~1だった確率値は-∞~0の値となります。最大値が0ということですね。上述の様に、確率pのような小さい値がp1*p2*p3…pnのように掛け算されると限りなく値が0に近づいてしまいますが、logを取るとlogの性質上以下のように、それを足し算に変換できます。
log(p1*p2*p3…pn) = log(p1) + log(p2) + log(p3) … + log(pn)
更に取る値も0-1という狭く小さい範囲ではなく-∞~0という広い範囲となるので、値が小さくなりすぎることも防止できます。
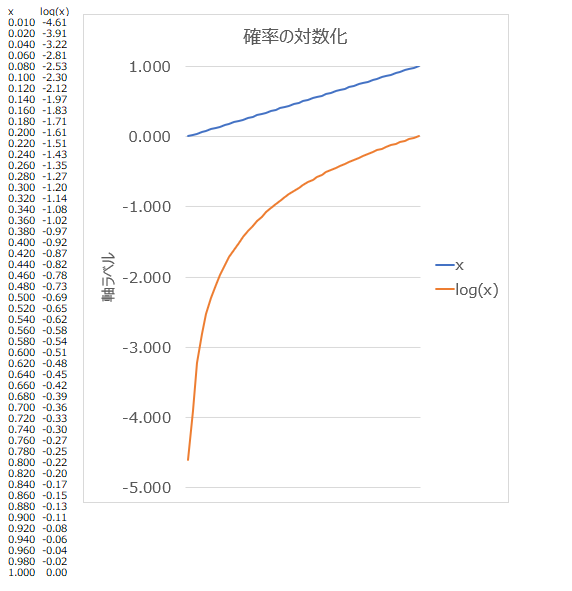
こうした理由で尤度を対数尤度に変更した上で、それらを掛け算ではなく足し算します。
最後に、なぜマイナスをつけるのか、ですが、これも便宜的な理由です。最小二乗法の記事で説明したように、機械学習の学習では基本的に”損失の最小化”を目指します。上記の対数尤度にマイナスをつけてやると、0~+∞の範囲となり、直感的に扱いやすいという理由で、マイナスをつけるのです。
ではこの項目の最後に、上から3人目までの対数尤度を合計し、マイナスをつけてみましょう。
log(0.96)=-0.0408
log(0.99)=-0.0100
log(0.38)=-0.9676
(-0.0408-0.0100-0.9676)*-1=1.0184
これが、ロジスティック回帰の結果を評価するための対数尤度です。上の表では対数尤度が16.63となっています。
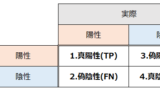
混同行列
上述の対数尤度を使うことで、あるwを前提とした予測値pがどれくらい尤もらしいかを評価できるようになりました。しかし、対数尤度は最終的なモデルの出力を評価するには使いにくい指標です。対数尤度が”5″だと高いのか低いのか、よくわかりません。
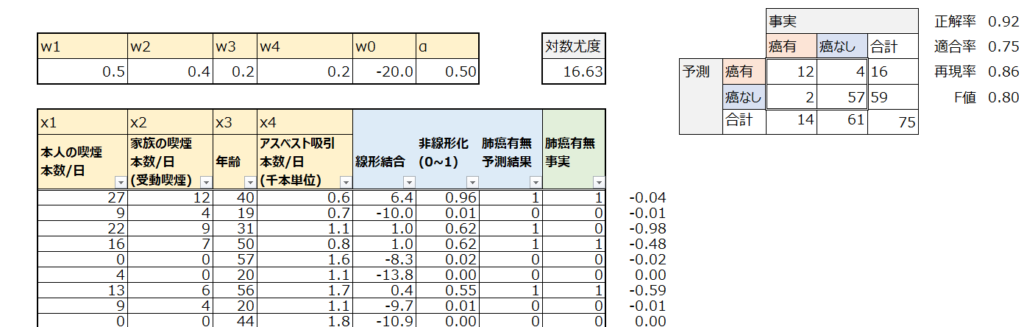
そこで、最終的な出力結果については混同行列を見た上で、正解率、適合率、再現率、F値などで精度を評価します。以下のように、正解率はなかなか高いですが、適合率がイマイチなので、癌の無い人を癌有りと予測してしまうケースが多いことがわかります。
混同行列や正解率、適合率などの指標については以下の記事を参照ください。
パラメータの更新(最適化)
上記にて、ロジスティック回帰の予測アルゴリズムと、その結果の評価方法である対数尤度や混同行列から得られる様々な精度の指標を説明しました。あと残るは、対数尤度の値が最小化になるようなパラメータを学習によって求め、その際の精度を確認するという作業です。
まずシグモイド関数のαはハイパーパラメータなので、人間が決めるものであり、学習による更新はありません。今回更新されるのは重みw1~w4とバイアス項のw0です。具体的には、勾配降下法を用いて更新します。勾配降下法については以下の記事を参照ください。
今回はExcelのソルバー機能を用いて以下のようにパラメータを最適化しました。手作業で設定したパラメータでは精度が低かった適合率の指標が改善しています。

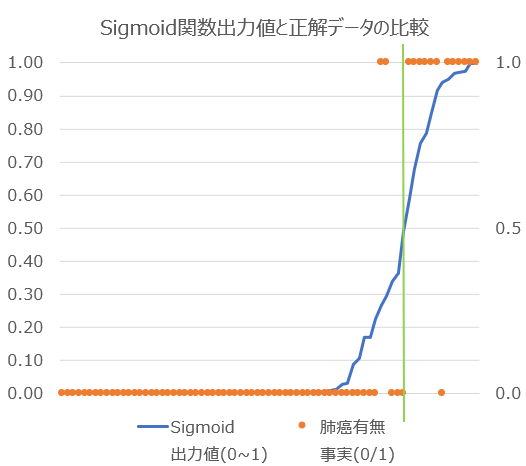
学習後のモデルが正解データをどのくらい正確に分類しているかをグラフ化しました。混同行列の結果からもわかる通り、ほとんどのケースを綺麗に分類できていますが、癌有2名と癌なし1名を誤分類していることがわかります。
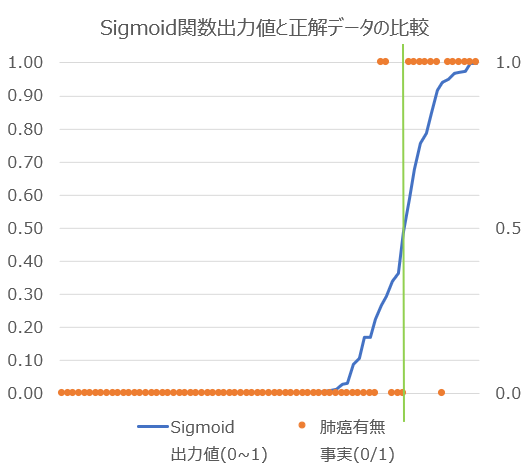
以上がロジスティック回帰の一通りの説明です。




コメント