【ディープラーニング】多層パーセプトロン

機械学習のモデルを過去にいくつか紹介しましたが、その中で単層のパーセプトロンについても解説しました。

この記事では、パーセプトロンを多層にすることで単層パーセプトロンでは実現できなかったXORゲートを実現できるようになることを説明します。なお、XORゲートについては以下の記事で説明していますので、参照ください。

多層パーセプトロン

多層パーセプトロンは、単層パーセプトロンの層を増やすことで、より複雑な処理を可能にします。ここでいう”層を増やす”というのは、ニューロンの数を増やすことだとイメージしてください。

ここでは例として、以下のようにバイアスと2つの説明変数のデータを重みづけした上で、重み付け和を青とオレンジの2つのニューロンに伝達し、それぞれのニューロンで重み付け和を閾値によって出力、その出力結果を更に別にニューロンに伝達し、そこでも閾値によって最終的な出力を決めるようなモデルを想定します。

入力・出力が複雑になり、単層パーセプトロンよりは人間の脳の構造に近くなってきましたね。なお、人間の脳におけるニューラルネットワークについては以下の記事を参照ください。

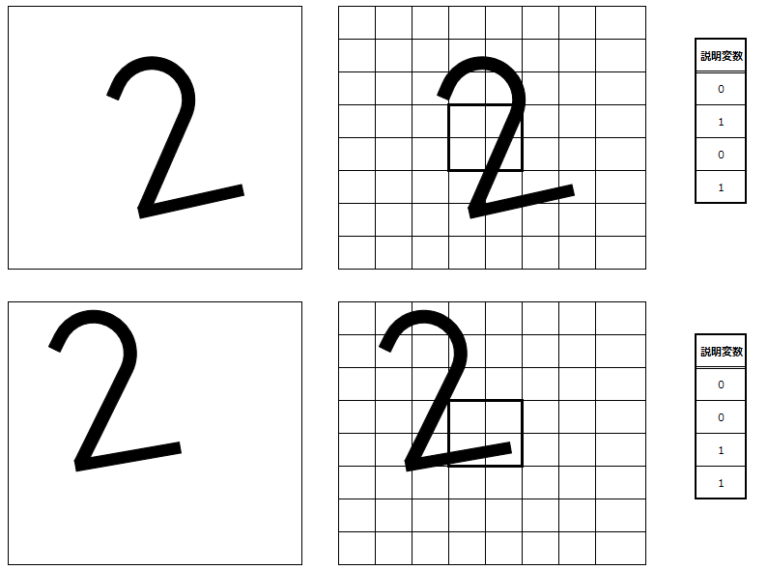
では、多層パーセプトロンを使った処理をできるだけ直感的に理解してもらえるよう例を出して説明します。以下の画像がアラビア数字の”2”であることは認識できると思います。この画像の”2”を、”2”の正解データであると仮定します。

この画像をモデルとして、8×8=64のマスで分解してみます。わかりやすいように単純化して説明しますが、この中で、太枠で囲われた真ん中の4マスに着目し、ここからデータが数字の”2”であるかを判別できるとします。

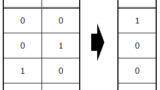
その4マスに以下のように番号を振り、黒い部分が一定以上を占めていれば”1″、そうでなければ”0″とします。この4マスの”0”または”１”を、今回の説明変数とします。

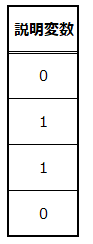
説明変数を表にまとめると、以下の通りになります。2番のマスと3番のマスを”黒”＝”１”と判定しています。

では、同じアラビア数字の”2”が以下のように書いてあったらどうでしょうか？

傾いていて、やや枠の右側に偏っています。

こちらも傾いていて、左上に寄っています。

この2つは、人間が見れば”2”と認識できるマスが、上述の4マスでAIに判定させるとどうなるでしょうか？以下に、元の画像と、マス目の画像、そして中央の4マスの説明変数を纏めています。

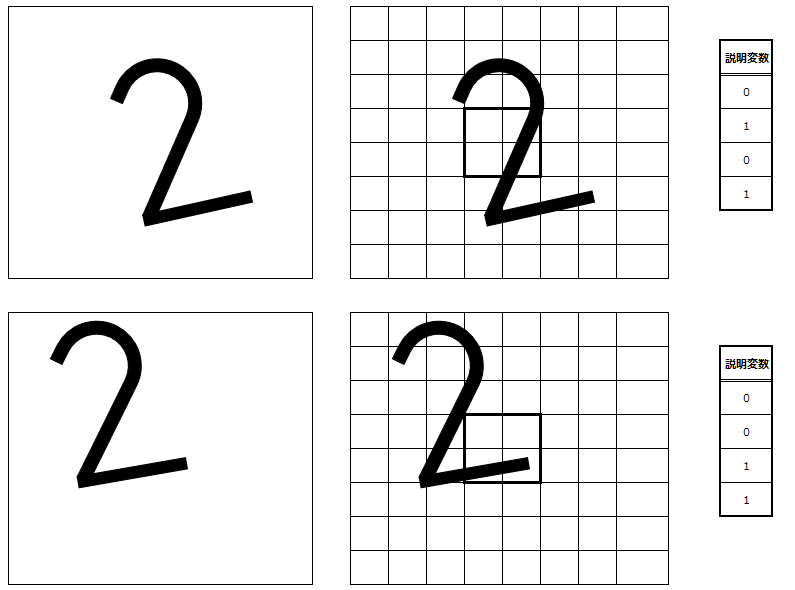
ここで、もう1度正解データの説明変数を確認してみると、以下のように、上の傾いている画像と説明変数の値が異なります。すなわち、このままでは上の2枚は”2”と判定されないということになります。

上の傾いた画像を、正解データと同じく”2”であると判定してもらうためには、ニューロンの層で閾値に従ったデータの変換が必要です。

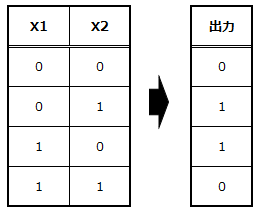
今回適用したい変換は以下の通りです。説明変数1をX1、説明変数2をX1としています。これは論理演算でいう”XOR(排他的論理和)”であり、単層パーセプトロンの項目で説明した通り、単層ではXORの変換が実現できません。

そこで以下のように、単層パーセプトロンで実現可能な変換をするためのニューロンを挟み、最終的にXORの変換を達成します。

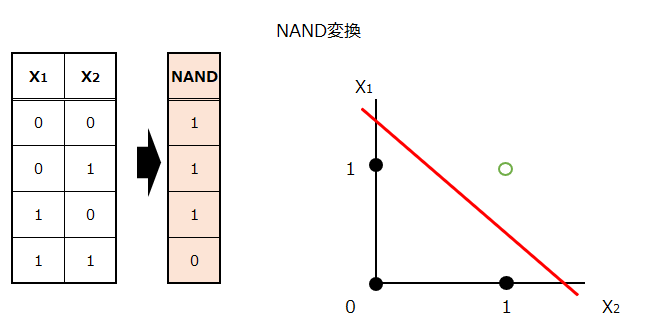
まずは、2つの説明変数をNAND変換します。理解をしやすくするために、グラフも示します。

次に、2つの説明変数をOR変換します。

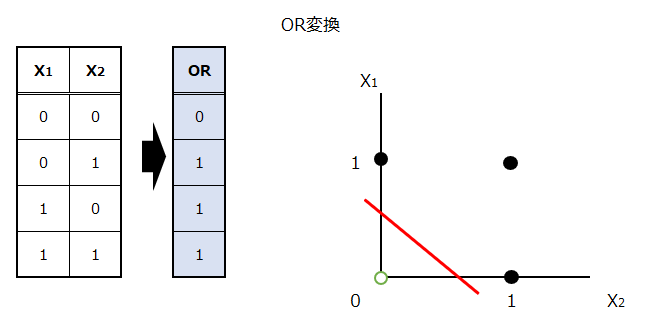
最後に、NAND変換した出力とOR変換した出力を新たな2つの入力として、AND変換を行います。

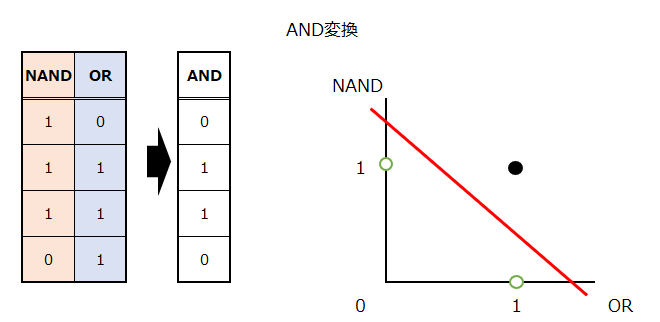
これで、綺麗に1本の線で分離することができました。これが線形分離可能、ということです。ニューロンを間に挟む、つまりパーセプトロンを多層にすることで、意図した線形分離が可能になったのです。

ところで、上の図ではわかりにくいですが、下の青枠部分は同じ値のデータが2つ重なっています。右側のグラフでは見た目上3つしかデータがないように見えますが、実際には白点が2つと黒点が2つです。

説明としては上記で理解してもらえると思いますが、では具体的には重みと閾値をどのように設定したらNAND変換、OR変換、AND変換を実現でき、結果としてXOR変換を実現できるのか、みてみましょう。まずは、以下が全体像です。

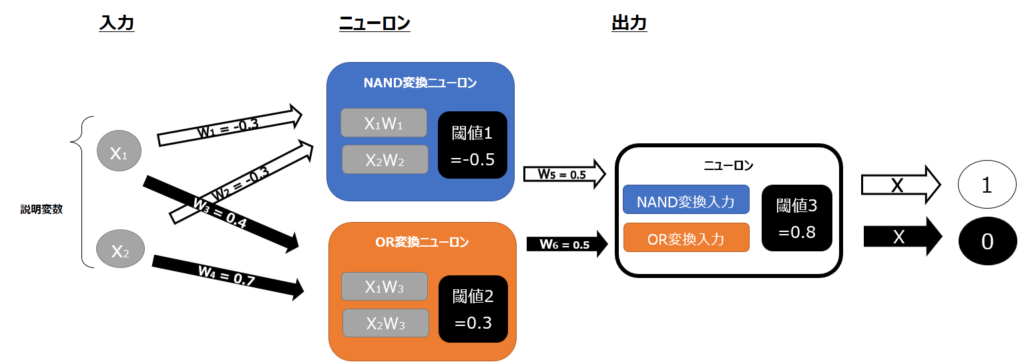
パラメータは以下の通り設定しています。

まず前半については、入力と出力が以下のようになっています。

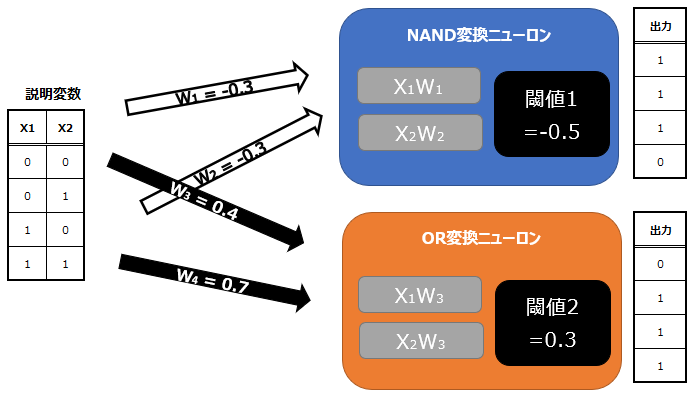
後半は以下の通りです。

余談ですが、上述の単層パーセプトロンではXOR変換ができないというのを納得できない方は、上記のパラメータを操作して単層でXOR変換が可能か試してもらえるとよいかと思います。

上述のように、パーセプトロンを多層にすることで、単層よりも複雑な処理を実現することができました。しかし、お気づきの方もいらっしゃるかもしれませんが、上記の変換は簡単な変換を繰り返しただけです。

実際にディープラーニングで行われているような複雑な変換処理を実現するには、パーセプトロンを多層にするだけでは不十分です。そこで、さらに複雑な処理を可能にするために用いられるのが、活性化関数です。活性化関数については今後詳細記事を掲載しますので、少々お待ちください。