前回の記事では勾配降下法の基本的な内容を説明しました。
今回の記事では、勾配降下法の問題について説明します。勾配降下法の問題としては、局所最適解に陥る問題と、勾配消失問題が挙げられます。
局所最適解とは何か
まずは、勾配降下法の問題として最も重要な局所最適解について説明します。
局所最適解と大域最適解
前回記事で説明した通り、勾配降下法では微分した値に学習率を掛けることである点においてどの方向にどのくらい進むかを決めていきました。これは裏返せば、微分した値が0になってしまえば、”進まない”、つまり終着点だと判断されるということです。
以下の図は、著者が仮のデータを元に作成した損失関数です。大きな赤い点がパラメータの初期値です。そこから勾配降下法を何度も繰り返し、小さな赤い点の付近でほぼ収束したとします。ここでいう収束というのは、勾配降下法のパラメータ更新を繰り返しても、パラメータの値がほとんど変わらない状況です。
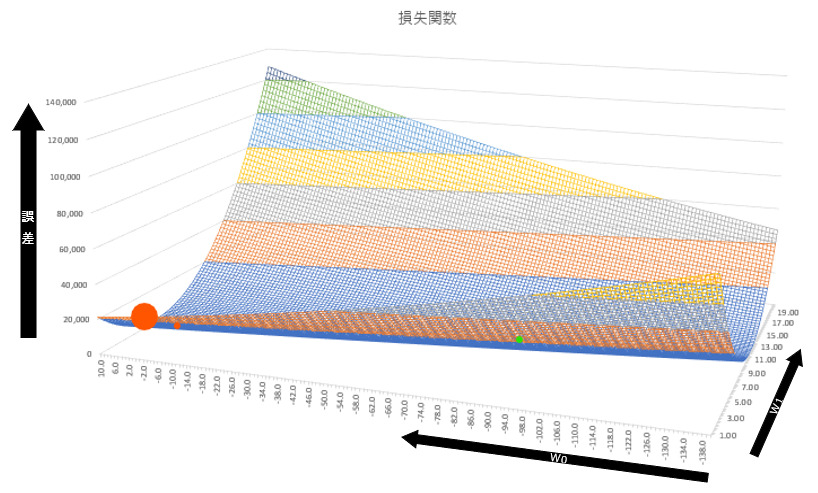
この収束した値が損失関数の本当の最小値であれば問題ないですが、そうではないことがよくあります。上の図でいえば、本当の最小値は薄い緑色で示した点です。特に横軸の値で大きな乖離があることがわかります。
この時、収束してしまった小さな赤い点を局所最適解、本当の最小値である薄緑の点を大域最適解と呼びます。
局所最適解の発生
まずは上の図が本当に局所最適解になっていることを確認してみましょう。上の図は縦軸の誤差が0~140,000と非常に広い値を取っているので、局所最適解になっていることがわかりにくいですね。そこで以下のように誤差を300~1,700と百分の一程度に縮小して細かく見てみます。
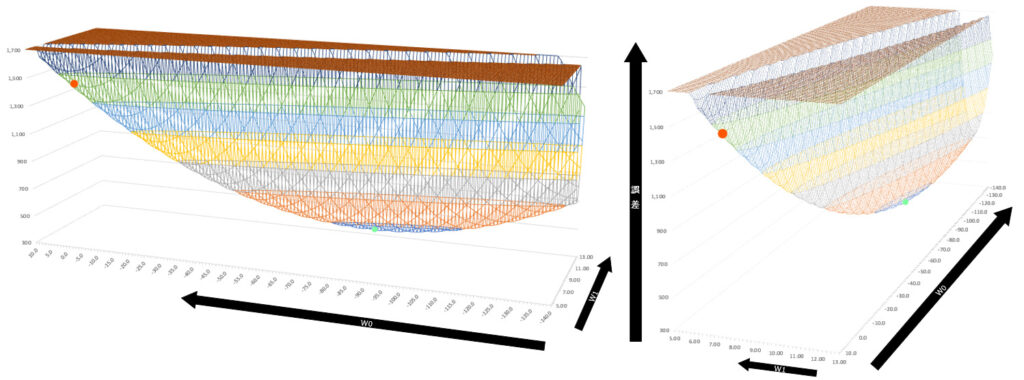
この図を見るとわかる通り、確かに赤い点と薄緑の点では誤差に大きな乖離があります。ではなぜ、こういった局所最適解が発生してしまうのでしょうか。
プラトー
以下の図は、初期値と局所最適解の赤い点に注目して横軸と奥行軸を入れ替えた図です。図からも直感的にわかる通り、局所最適解の場所ではほぼ平面になっていることがわかると思います。
ここで注意すべきは、下図の誤差は0~30,000の範囲で表示していますが、上で局所最適解を示した図は誤差を300~1,700という狭い範囲で示している点です。ここからもわかる通り、本来は下図の奥行軸であるw0に関して大きく改善の余地がありますが、w0と比較してw1方向の勾配の変化が非常に大きいため、パラメータ更新をしてもw1方向で傾きが0になるような点で収束してしまうのです。

上の図のように、本来の最小値ではない平坦な場所で収束してしまうような状態をプラトー(Plateau)と呼びます。
勾配消失問題
次に、ディープラーニングのようにニューラルネットワークを用いた機械学習の場合に発生する勾配降下法の問題として、勾配消失問題を紹介します。なお、この項目はディープラーニングについて知っている方が理解しやすいかもしれません。ディープラーニングについての詳細は以下を参照ください。
ニューラルネットワーク
ディープラーニングというのは一言でいえば、例外もありますが、ニューラルネットワークによって人間の脳の活動を真似することで、従来の機械学習では実現できなかった複雑なモデルを構築することであると言えます。
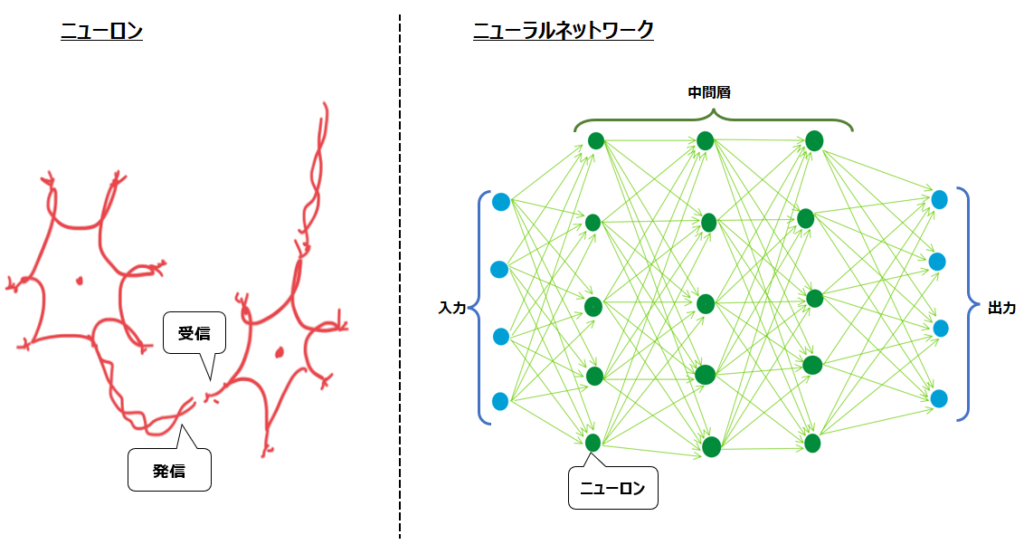
人間の脳には、上述のニューロンが800億個以上存在すると言われています。その800億個のニューロンそれぞれが、発信部と受信部の間のシナプスと呼ばれる構造を介して情報の伝達をしています。シナプスの大きさ(=ニューロン同士の結合の強さ)はそれぞれ異なり、人間が繰り返し学習すると特定のシナプスが大きくなったり、新しいことを学習するとシナプスの形が変わったりします。
大きな(=強い結合の)シナプスを介した信号のやりとりでは、発信側のニューロンからの伝達物質が強くなり、受信側の神経が興奮して電気を流すことで、更に後続のニューロンまで信号が伝達されていきます。反対に小さなシナプスでは後続ニューロンに信号が伝達されません。
こうした複雑な処理を経てはじめて人間は、例えば初めて見たものを正しく認識できます。このようなニューロンの複雑なネットワークのことを、ニューラルネットワークと呼びます。
活性化関数と誤差逆伝播
ニューラルネットワークにおいては上図の矢印1つひとつが重みパラメータです。これらの値をどう更新するかを決めるのに、勾配降下法を用います。前回記事でも説明した通り、勾配降下法では微分によって勾配を算出し、それに基づいて重みをどのように更新するかを決めます。
ここで問題になるのが、活性化関数です。活性化関数というのは、ニューラルネットワークの中間層において、重み付き線形和を何らか変化させるための関数です。例えば活性化関数にシグモイド関数を用いる場合、以下のように出力値は必ず0-1となります。
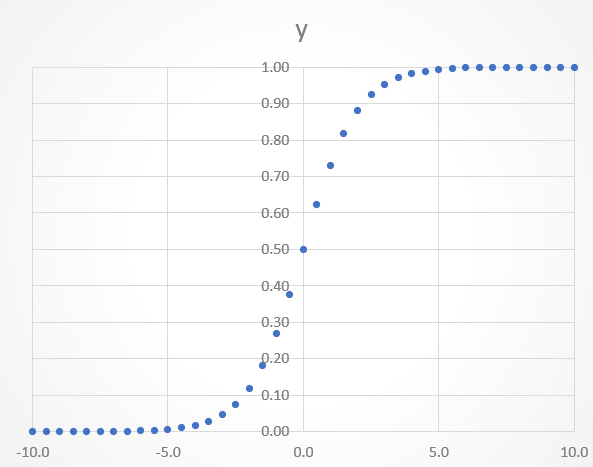
この関数は分類問題で確率を出力するのに便利です。色々なデータを入力し、重みをかけたものを、最終的に確率0.8、といったように直感的にわかりやすい形で出力できます。
一方、勾配降下法による勾配計算においてこの関数の出力値を微分すると、問題が発生します。それを説明するために、簡単に誤差逆伝播について説明します。
損失関数の微分を計算することで重みを更新するのが勾配降下法ですが、例えば以下の赤い矢印の重みを更新するにはどうすればよいでしょうか?
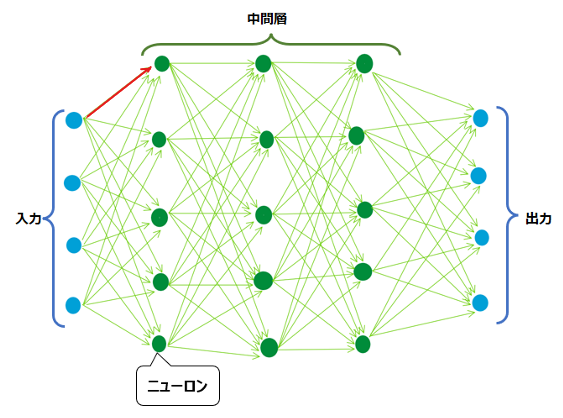
微分、つまりこの赤い矢印が少し変化した時に出力と正解のどのくらい誤差が変わるかを調べるには、何とその先の青枠内のすべての部分について計算し直さないといけません。赤い矢印が変化したら、その先もすべて何らか変化が生じ、誤差の値に影響を与えるため、赤い矢印の変化による誤差の変化を計算するには、その先の工程も計算し直す必要があるのです。
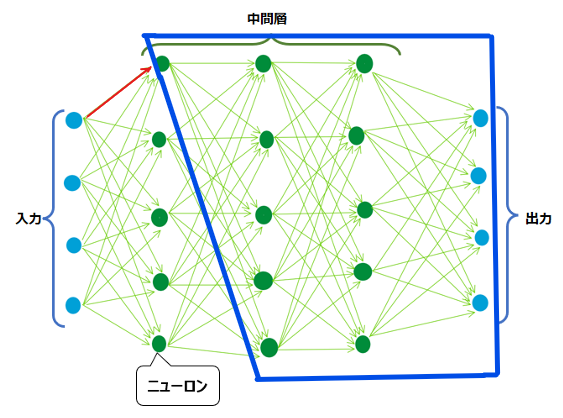
上の図のように、矢印(重み)1本について考えるだけでも微分の計算コストが高いですが、勾配降下法においてはすべての重みについて微分の作業を行わないと、更新ができません。上のような単純な構図であっても、すべての重みについて微分する計算コストがどれほど高いか容易に想像がつくかと思います。さらに、ディープラーニングにおいては入力と出力が10,000個、中間層も数100層存在するようなことがあります。これらの計算コストは果てしなく高くなります。
そこで使用されるのが、誤差逆伝播法(バックプロパゲーション)です。この手法では、微分の計算を式変形によって簡略化し、また出力層から入力層に向かって後ろから計算していくことで計算コストを下げることができます。誤差逆伝播法については今後の記事で解説しますので、お待ちください。
勾配が消失する
ここで、勾配降下法による勾配計算においてこの関数の出力値を微分すると、問題が発生するという話に戻ります。誤差逆伝播法では、出力層における微分値を中間層において使用します。微分された値がどんどん入力層側に渡されていくということです。
ここでシグモイド関数がどのような関数だったかを思い出してみます。出力値は以下のように0-1の間ですが、傾きは0-0.25の間で変化します。つまり、シグモイド関数を適用した値を微分すると、最大でも0.25にしかなりません。更にこの値が誤差逆伝播の流れに沿って次に渡して微分していくと、その値はどんどん小さくなっていき、いずれは限りなく0に近づいていってしまいます。

すると、中間層の数が多いと、入力層に近い層ほど誤差が0になってしまい、勾配降下法による重みの更新がうまく実行されず、モデルの精度が高くならないという問題が発生するのです。これが、勾配消失問題です。
勾配降下法の種類
以上述べてきたように、勾配降下法にも問題があります。前半で紹介した大域最適解に辿り着けない問題にうまく対処するために、勾配降下法には様々な種類があります。今後の記事で勾配降下法の種類についても解説しますので、お待ちください。
後半の勾配消失問題についてはディープラーニングの関連記事で今後扱います。


コメント