主成分分析(PCA:Principal Component Analysis)は、AI・データサイエンスの分野で次元削減ために用いられる統計的手法で、元のデータの中で最も大きな変動を捉える主成分(PC, Principal Component)と呼ばれる無相関の変数を新たに見つけることで、データセットの次元を小さくします。
まずは、次元削減から説明します。
次元削減とは何か
次元削減(dimensionality reduction)とは、AI・データサイエンスの分野で、特徴や変数の数を減らして大規模なデータセット内の最も重要な情報や関連する情報を特定し、データを最もよく表現する次元のみを保持することで、データセットを要約する手法です。
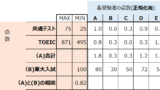
具体例を出して説明します。あるクラスAでテストが行われ、以下のような結果が得られたとします。この結果から生徒と科目の関係性を把握したいと思ったとき、このままでは科目数が多すぎて、どのような関係性があるのか理解するのが困難です。この場合の科目数が、上で説明した”特徴”や”変数”の数に該当し、それをデータサイエンスや数学の文脈では”次元”と呼びます。
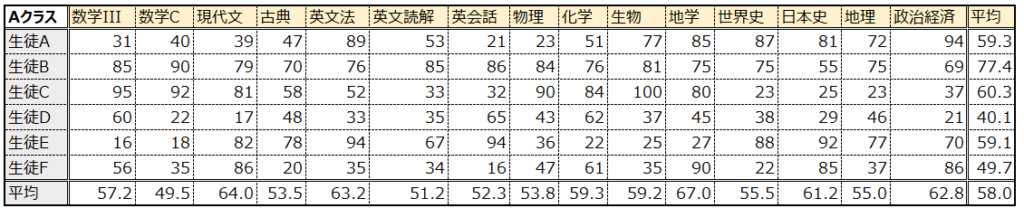
ではこの時、”科目数”つまり次元を削減できるとどのようなメリットがあるでしょうか?これを実感するために、以下では次元を15から6に削減してみました。削減方法は、話を簡単にするため、いくつかの科目を纏めて平均しています。

6次元であれば、全体の傾向が見えてくると思います。例えば生徒Aは暗記科目に強そう、生徒Bは全体的に得点が高い優等生、生徒Cは理系科目に強い、生徒Dは全体に得点が低い劣等生、生徒Eは文系科目に強く、生徒Fは英語に弱点有、といったところです。
更にこれをヒートマップのように表示すると、上の特徴がより明瞭になります。

更に、次元を2まで落とします。
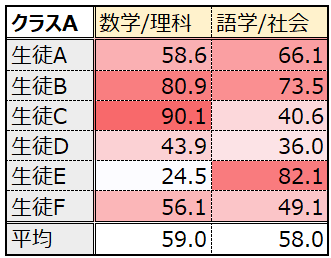
2次元の場合は、散布図で可視化することもでき、こうするとデータの構造を人間が直感的に理解することもできるようになります。

このように、人間が目視で見たり、手作業で分析を実行する際にも次元削減は有効ですが、コンピュータに分析をしてもらう機械学習の分野でも、次元削減は処理しなければいけないデータ数を少なくすることで、計算量を削減したり、不要なデータを無視することで精度が向上したりするのです。
BMIの例
我々の日常生活においても、次元削減による情報の圧縮は見られます。有名な例としては肥満度を測るためのBMIが挙げられます。BMIは体重÷(身長)^2で計算されます。つまり、元々体重と身長という2つの別々の指標を、BMIという1つの指標に纏めることができるようになっています。
体重や身長は、それだけでは肥満度を知ることはできません。”体重80kg”で肥満の人もいれば、そうでない人もいます。”身長150cm”の人も、それだけで肥満レベルを知ることはできません。しかし、それらの情報を合わせた”BMI 35.5″は、肥満レベルがそれなりに高いことを示してくれます。
BMIの例をさらに使って、次元削減のメリットを紹介します。健康志向の高い人は、以下のように体脂肪率とBMIを使った肥満レベルのマトリックスを見たことがあると思います。
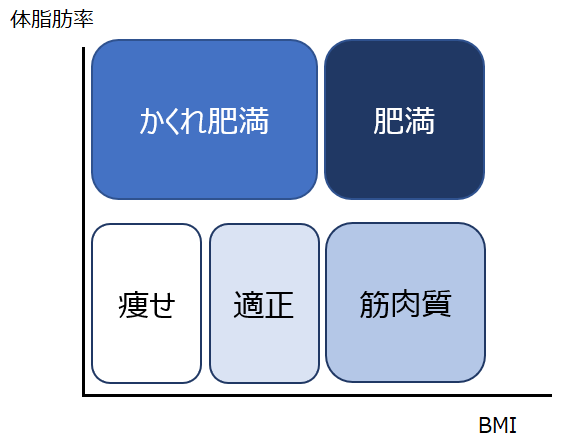
BMIだけでは、”アスリートのように筋肉の多い人脂肪が多い人を区別できない”というデメリットがありますが、表のように2軸で評価することによって、非常に解像度高く肥満レベルをカテゴライズすることができます。この表を、BMIの代わりに”身長”と”体重”によって表現すると、体脂肪率と併せて3軸(x軸y軸z軸)が必要になり、直感的に理解しずらくなってしまいます。
以上が、BMIからわかる次元削減のメリットです。
主成分分析のイメージ
続いて、次元削減の手法である主成分分析について説明します。
主成分分析は、“分散の最大化”によって次元削減をします。より具体的には、説明変数間の相関関係から”主成分”と呼ばれる新しいベクトルを生成する際に、データの分散ができるだけ大きくなるようにします。
いきなりアルゴリズムを説明しても意味が分からないと思うので、まずは次元削減の項目で示した点数表から5科目を抽出した以下の表を使って、主成分分析による次元削減がどんなことをしているの、具体的なイメージを示します。
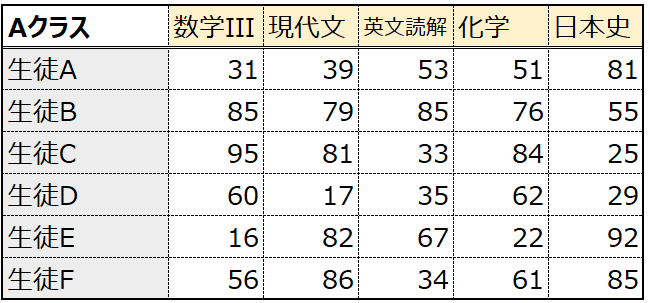
このデータに対して、新たなベクトルw(後述の主成分、固有ベクトル)を生成し、”理系指数“と”言語指数“を作成してみました。ここでベクトルwは、”理系指数“と”言語指数“を作成するために、各科目の点数に重み付けをしています。
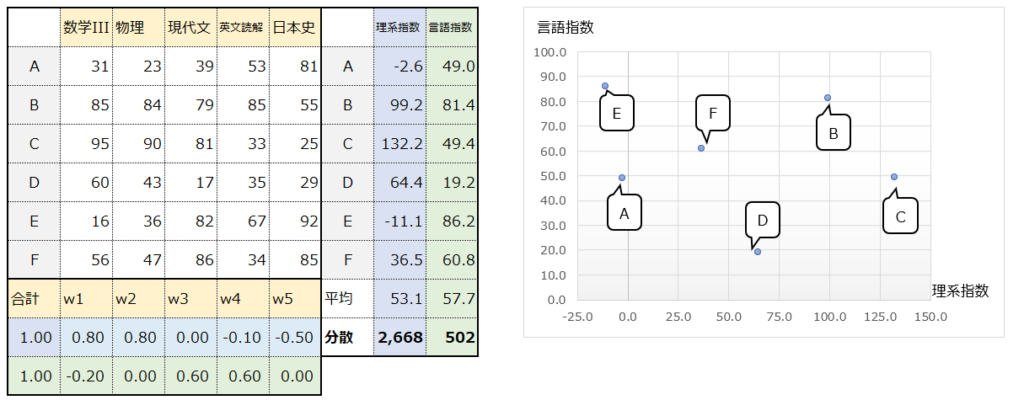
具体的に見てみます。生徒Aの”理系指数”は-2.6と計算されていますが、これは生徒Aのテストの点数とベクトルwの総和で、以下のように計算されています。数学III・物理の点数を高く評価し、日本史の点数を低く評価するようになっています。
31*0.8 + 23*0.8 + 39*0.0 + 53*-0.1 + 81*-0.5 = -2.6
生徒Bの”言語指数”は81.4と計算されていますが、これは以下のように計算されています。数学IIIを低く評価し、現代文と英文読解の点数を高く評価しています。
85*-0.2 + 84*0.0 + 79*0.6 + 85*0.6 + 55*0.0 = 81.4
5科目の点数を”理系指数”と”言語指数”という2次元のデータに次元削減したことで、右図の散布図のように可視化することができ、わかりやすいですね。
ではこの時、ベクトルwの値をどのように決めるかというと、主成分分析では”理系指数”や”言語指数”のような値(後述の主成分スコア)の分散(後述の固有値)を最大化することと、その際の制約条件としてベクトルwの合計値を”1″に固定することによって決定します。
以下で順に解説します。
分散の最大化
まず分散を最大化するという点ですが、例えばベクトルwの設定次第では、以下のようにより分散が少ない値(363と235)を取り得ます。主成分分析では、下の表よりも上の表の方が分散が大きいので、上の表のベクトルの方が”良い”ということになります。
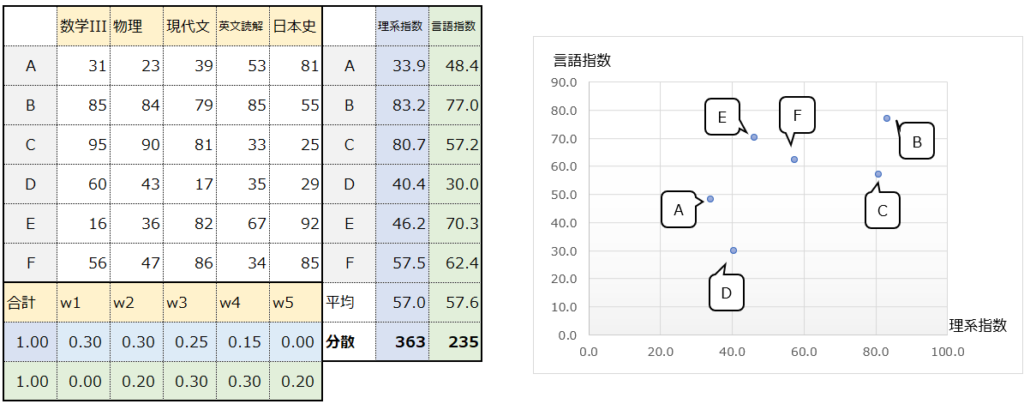
“分散が大きい方が良い”というのがイメージし難いかもしれません。ここでは、”分散が大きい方が情報量が多いので重要”と捉えると理解しやすいかもしれません。
例えば、”手の指の本数”というデータは、ほとんどの人が”10″で、分散が非常に小さくなるはずです。これは、聞いても聞かなくても、ほとんどの人がわかっている情報と言うことで、”情報量が少ない”と言えます。一方、”年収”や”身長”は人によって様々で、分散もそれなりにあるはずです。分散があるからこそ、”情報量が多い”と言えます。
理解のために、敢えて極端な例を出します。以下は分散を最小化するようにベクトルwの値を設定してみました。ほとんどの生徒の理系指数と言語指数が同じ値になっています。”分散が小さい=情報量が少ない”というのが直感的にイメージできるのではないでしょうか。
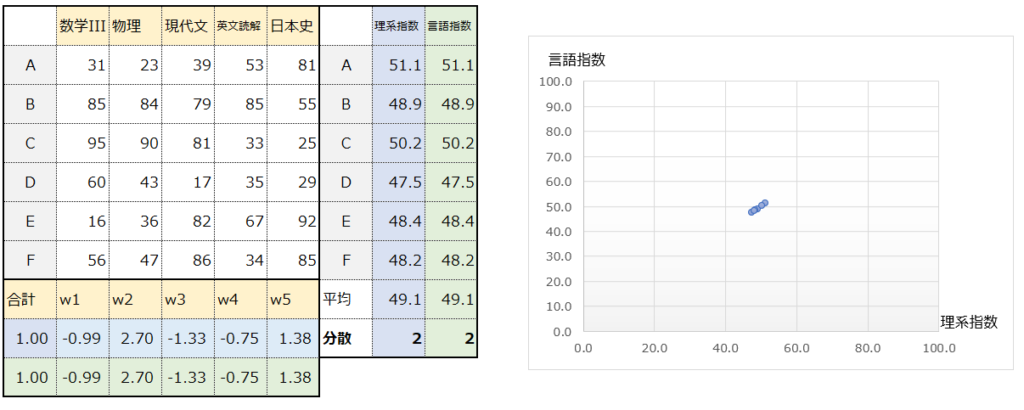
ベクトルwの総和=1
続いて、なぜベクトルwの総和を1に固定するのかを説明します。上で示した例を再掲します。
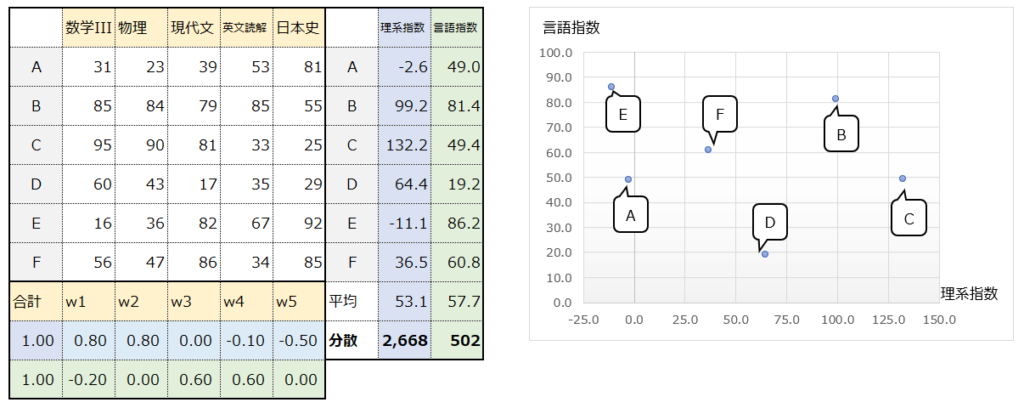
この時、ベクトルの総和を1に固定しないとどうなるでしょうか。例えば以下のように、全ての値を10倍すると、分散は100倍となります。分散は大きくなりましたが、本質的に”理系指数”と”言語指数”の情報量は増えていません。
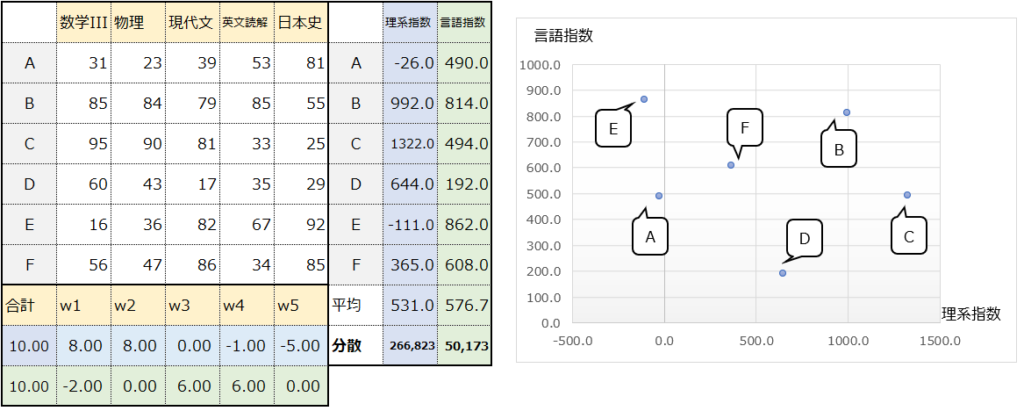
このように、ベクトルの値をただ大きくするだけで分散が大きくなっても、それは主成分分析で本位とするところではありませんので、ベクトルの総和を1に固定することで、適切なベクトルの値を考えることができるのです。
主成分分析の具体例
では、具体的に、主成分分析を実行してみます。上の項目では5項目のみ抽出していましたが、再び全科目の表を使います。

まず生徒の点数については以下のように標準化しました。

標準化については以下を参照ください。
第1主成分の求め方
この点数表のデータに対して、科目ごとの主成分(科目数分の成分を持つ固有ベクトル)を調べると、以下のようになります。はじめに算出したので、この固有ベクトルを”第1主成分”と呼びます。

このベクトルの値はRやPythonなどプログラミングやExcelのソルバーを使って求めることができますが、自分の手で計算する場合にはラグランジュの未定乗数法という大学数学の知識が必要になりますので、ここでは説明は割愛します。
またこの固有ベクトルの値は、上述の様に主成分スコア(点数とベクトルの値の総和)の分散(固有値)を最大化する値になっています。

ではこの値をどのように解釈できるでしょうか。まず第1主成分は、理系科目を低く評価し、文系科目を高く評価しているように見えます。つまり第1主成分は値が高いほど”文系”寄り、低いほど”理系”寄りと言えそうです。
そして第1主成分のスコアを見ると、生徒E=>生徒Aの順で高く、この二人が文系が寄り、生徒Cが理系寄りであることわかります。
第2主成分の求め方
続いて、第2主成分を求めます。基本的な考え方は第1主成分と同じですが、唯一の違いは既に算出した第1主成分の主成分スコアとの相関係数が0に近づくような値を設定するという点です。

なぜ相関係数が0でないといけないのでしょうか。
これは、相関係数が1もしくは-1に近い状態を考えることで納得できます。まず相関係数が1に近いというのは、第2主成分の値が第1主成分と等しいもしくは近しい状態です。同じ分析をしているわけですから、この第2主成分に意味がないことはすぐに理解できると思います

では、相関係数が-1に近いのはどのような状態かと言うと、第1主成分を-1倍した状態です。これは言い換えると、第1主成分を”文系レベル”にし、第2主成分を”理系レベル”としているということです。理系レベルの高さを知りたかったら第1主成分のマイナス値を見ればよく、この第2主成分は不要です。
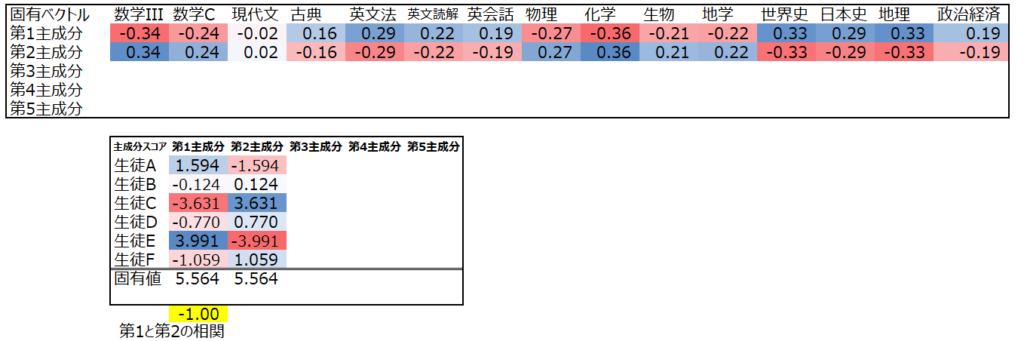
このように、主成分スコア同士が相関してしまっているということは、既に算出した主成分と同じような分析をしてしまっているということになります。第2主成分を第1主成分と全く異なる視点からの分析とするために、第1主成分と相関していない固有ベクトルを設定する必要があるのです。
なお、相関係数については以下の記事を参照ください。
第3主成分以降の求め方
同様に第3主成分以降も算出できます。第3主成分以降も、既出の主成分との相関が0に近づくように固有ベクトルを設定します。
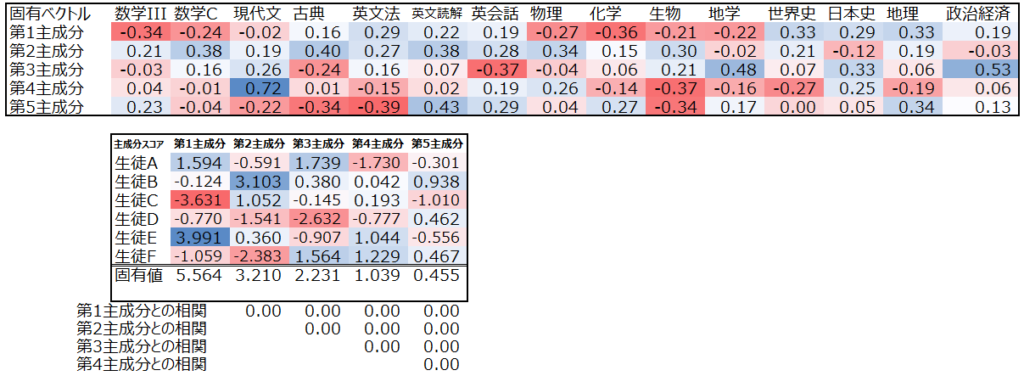
では、この主成分分析の結果をどのように解釈できるでしょうか。既に述べたように、第1主成分は”文系優位レベル”と言えそうで、逆に言えば第1主成分から理系優位レベルもわかります。一方、第2主成分は成績悪い人が点数低い科目(数C・古典・英文読解・生物)を高く評価しており、成績優秀者のポイントが高くなるようになっていると言えるかもしれません。
第3主成分は、政経・地学・日本史を高く評価し、英会話と古典を低く評価しています。生徒AとFに共通する何かを捉えているようですが、人間にはこれがどんな意味なのかわかりません。
以上が、主成分分析の具体例です。
主成分分析の結果をどう見るか
上記にて、主成分分析の具体的な内容を紹介しました。では次に、主成分分析の結果をどのように見ればいいか、そのために有用な寄与率と主成分負荷量を紹介します。
寄与率
寄与率は、各主成分が固有値にどれだけ寄与しているかを測るものです。
これを理解するには、そもそも主成分分析において固有値がどのように解釈できるかを考える必要があります。上記では説明しませんでしたが、主成分分析の固有値(分散)の合計は本来変数の数に一致します。今回は15科目のテスト点数データで変数が15個あるので、主成分を全て出せば合計が15となります(表中では簡単のために第5主成分までしか出していないので合計が15に満たず12.5ですが)。
更に言えば、固有値の値は、その主成分が変数のいくつ分を説明できているか、を表します。今回の第1主成分の固有値は5.56ですから、この第1主成分だけで全体の1/3強を説明できているということです。
その前提で、寄与率は以下のように計算されます。
寄与率 = ある主成分の固有値 / 全ての固有値の合計
この寄与率が高いほど、対応する主成分が固有値、つまり元データのばらつきを記述する上でより重要であり、言い換えると多くの情報を表現していることを意味します。つまり、寄与率は、どの主成分が元のデータを要約する上で重要であるかを理解するのに役立つのです。
更にこの寄与率を、大きい順に累積した累積寄与率という指標も存在します。累積寄与率は0.8-0.9が望ましいとされていて、これはつまり、全体の80%-90%を説明できるように主成分によって次元削減をするべし、ということになります。

今回の例では、第4主成分までで累積寄与率が0.8を超えていますので、元々15科目あった15次元のデータを、4次元まで落とすことができることが示唆されます。
負荷量
負荷量(因子負荷量、主成分負荷量)は各主成分と元の変数の相関係数で、各主成分と元の変数がどのように関連しているかを解釈するために使用されます。
今回の例では、得られた5つの主成分と、元の15科目がどのように相関しているかを見ることができます。固有ベクトルの値からもこれらの関係は見えてきますが、相関係数とすることでより直感的に理解しやすい数字となります。

なぜ主成分分析が教師なし学習なのか
上述の様に主成分分析はデータからパターンを学習するプロセスを含むため、機械学習手法の一つとして紹介されることも多いです。より具体的には、あらかじめ定義された正解ラベルやカテゴリを持たないので、教師なし学習の一つと言えます。教師なし学習については以下を参照ください。
主成分分析で”正解ラベル”がないというのはイメージし難いかもしれません。元々科目のラベルは確かに存在しますが、最終的に主成分分析で得られるのは”主成分”です。上記で説明したような”文系レベル”を表す第1主成分は、予め人間が指定したわけではなく、主成分分析の計算結果が出てから、人間が事後的に解釈しているに過ぎません。同じようなテストデータに対して主成分分析を実行しても、毎回”文系レベル”を表す主成分が得られるとは限らない点に注意しましょう。
なお主成分分析は、最も重要なパターンを保持したまま入力データの次元を下げることができるため、様々な機械学習タスクに有用です。例えば、探索的データ分析、特徴抽出、データの可視化などに利用することができます。また、主成分分析は、クラスタリングなどの他の機械学習手法を適用する前に、入力データの次元を小さくする前処理として使用することもできます。


コメント