正規分布とは、以下の確率密度関数で表される確率分布の一つです。この数式のざっくりイメージや、正規分布がどういったデータに当てはまるかを解説します。

正規分布の関数の由来
正規分布の数式の意味については、既に多くのページで解説されています。例えば以下のページを参照ください。

一方この記事では、普段数学を使っていない人が直感的にイメージできるような補足説明をします。
平均値にデータが多くなるような数式を探せ
正規分布の複雑な数式のスタートは、世の中にありふれた事象である”平均値付近にデータが多くて、平均値から離れるほどデータが少なくなるような数式”を作れないか、というものでした。
そこでまずは、ネイピア数を使った以下の数式が、形として優れていると発見されました。”この数式が使えるんじゃない?“という発想です。

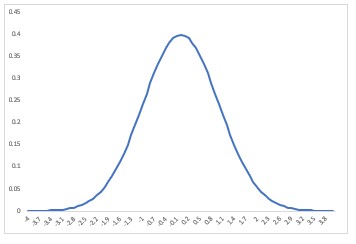
グラフを描いてみると、以下のようになります。確かに、よく見る釣鐘型と同じような形状ですね。
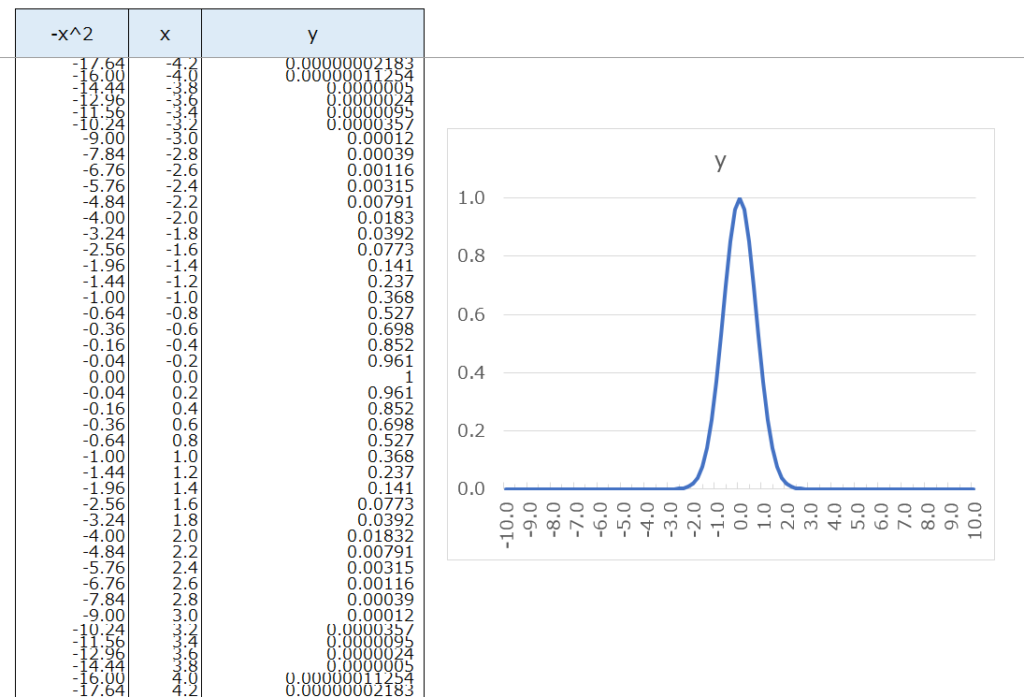
改良してみる
次に、上の数式をベースに更に使い勝手がいいように以下の改良を加えます。
- ①平均値を好きな値に設定したい
- ②標準偏差(データの塊具合またはバラバラ具合)好きな値を設定したい
- ③確率密度関数として使いたいので、全範囲の確率点の和が1になるようにしたい
まず①②の意味ですが、①は分かりやすいと思います。平均点が40点のテストでも60点のテストでも、この正規分布の性質を利用できるような数式が欲しい、ということです。③についてはこの記事で解説すると詳細に入り過ぎるので、冒頭で紹介したような記事を参照ください。
②はもっとなだらかとか、もっと尖った分布でも使えるような数式が欲しい、ということです。例えば同じ平均点50点でも、標準偏差10より標準偏差15のテストの点数の分布はなだらかで、平均点から離れた点数の値も多く存在します。
まずは①②について考えるために、元の数式を思い出します。

シンプルな数式ですが、この数式では平均0、標準偏差1になっていると捉え、以下のように書き直してみます。分母を2乗しているのは、標準偏差がどんな値でもプラスになるための措置です。
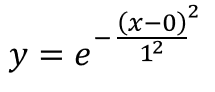
この状態では以下の通り、山の頂点は平均値である0であり、標準偏差1分の幅を持っています。

ではこの数式を使って、平均2、標準偏差3を表現してみるとどうなるでしょうか。数式は以下の通りです。

グラフにすると以下の通りです。元の平均と標準偏差を黒で、新しい平均と標準偏差を赤で表示しています。平均値が左に移動し、標準偏差の分山もなだらかになりました。使えそうな雰囲気になってきましたね。

ここまでの内容を一般化すると以下のようになります。μ(ミュー)は平均値、σ(シグマ)は標準偏差です。だいぶ完成計が見えてきましたね。
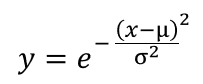
この時、ネイピア数の乗数の分母は、2倍しておくと後々計算が簡単になるという事情があるので、2倍しておきます。

これで、実は8割がた完成しています。あとは、ネイピア数の前にくっついている(掛け算されている)定数のみですね。
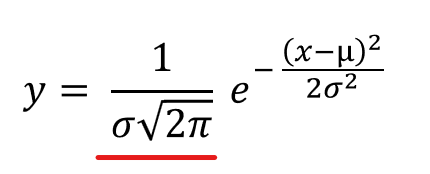
これは上述の③確率密度関数として使いたいので、全範囲の確率点の和が1になるようにしたい、という作業から必要になります。まずは直感的な説明として、すべての起こりえる可能性を足したら1になるということは理解できると思います。サイコロの各目の出る確率は1/6で、すべて足すと1(1/6 x 6)になりますよね。コインも表裏共に出る確率は1/2で、足すと1(1/2 x 2)になります。
後は詳細は省略しますが、積分したら1になるような定数が、計算したら1/σ√2πだった、ということです。ざっくりですが、これで”正規分布を表現する数式を作れた!”ということになります。
正規分布が当てはまるもの
では、以下の釣鐘型の正規分布は実際に世の中のどのような事象に当てはまるのでしょうか。

そもそも”正規“分布という名前は、この分布がデータサイエンスの分野で最も標準的な分布だと見做されていることによります。ですから、様々な事象において正規分布が観測される”はず”です。
例えば身長があります。以下から小学生~高校生の身長の分布を確認できますが、綺麗な正規分布になっていることがわかります。
https://www.mext.go.jp/component/b_menu/other/__icsFiles/afieldfile/2013/03/29/1331750_1.pdf
また大規模なテストの点数は正規分布することが知られています。だからこそ、受験期には標準偏差を用いた指標である偏差値をチェックするのですね。
更には、液体や気体中の微粒子がランダムに動く現象であるブラウン運動も、その運動量は正規分布に従うことが知られています。
ではなぜ、多くの事象で正規分布が観測されるのでしょうか。それは、身長やテストの点数といった事象は、様々な因子がお互いに無関係に影響を及ぼすからです。こういったそれぞれ無関係なもの同士の足し算で起こるものを加算過程と呼び、加算過程で発生する事象では後述の中心極限定理により正規分布が現れることがわかっています。
例えば身長を決める要因がたくさんあり、Aが遺伝子、Bが年齢、Cが居住地域、そのほか因子がZまであるとしましょう。この時、それぞれの因子は、互いに強く影響されているわけではないですよね?ある遺伝子の場合に年齢は20歳だとかいうことはありませんし、遺伝子と居住地域は少しは関係があるかもしれませんが、直接的な関係ではないことが見込めます。
こういったそれぞれ独立の因子の積み重ねで結果が分かれていくような加算過程の場合は、正規分布になりやすいのです。
中心極限定理
上述の中心極限定理というのは、サンプルサイズが大きくなるほど、標本平均の分布は正規分布に近づく、というものです。標本平均というのは母集団から抽出した一部のデータの平均値のことです。
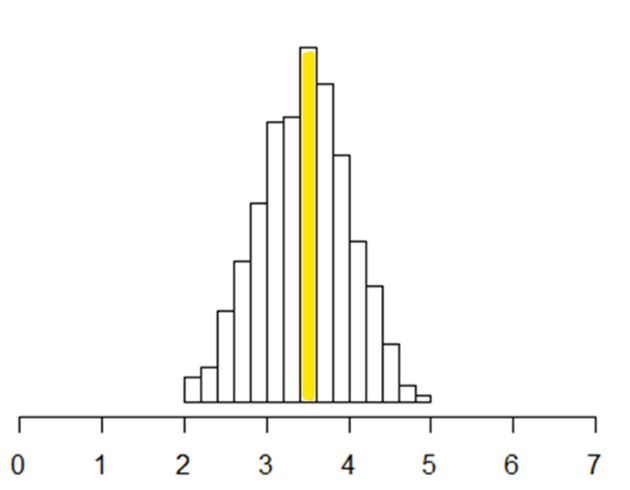
例えば世の中の全てのサイコロ(母集団)を持ってくることはできないが、サイコロを振る(標本)作業を繰り返すと、サイコロの目(標本平均)の平均値は3.5に近づき、その分布は釣鐘型になる、というものです。
正規分布が当てはまらないもの
一方、正規分布が当てはまらない事象というのも、意外とこの世には多く存在します。”正規分布”を前提としたさまざまなデータサイエンスの手法を使うとき、以下のようなケースがありえることを念頭に置きながら使うべきでしょう。
べき分布
まずはべき分布を紹介します。べき分布というのは以下のように、ある値のべき乗を取るような分布です。

以下のページでべき分布の例として、月のクレーターのサイズや地震の規模と頻度、株価の変動幅などが紹介されていますので参照ください。
べき分布で理解しないといけないのは、正規分布の中心部分のような”ここが平均的な値”というエリアが存在しないということです。平均値と標準偏差という指標で特徴を掴むことができず、非常に扱いずらい性質であると言えます。
対数正規分布
また、ある値の対数を取って分布を取ると正規分布しているようなデータがあり、それらを対数正規分布と呼びます。対数正規分布はxをそのまま使う場合は以下のような形をしていますが、
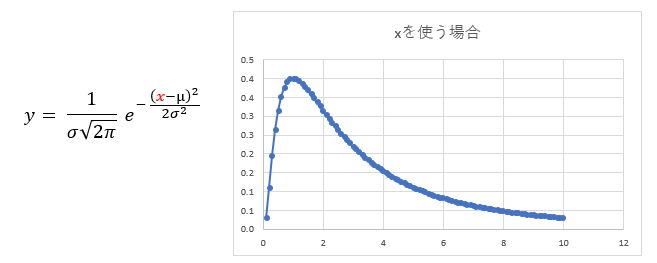
文字通り、元の正規分布の関数のx部分を以下の通りlog xに変更すると、以下のように正規分布のような形になります。

これが対数正規分布です。上で正規分布の原因として加算過程を紹介しましたが、各要因が互いに影響しあうようなものを乗算過程と呼び、その結果は正規分布ではなく対数正規分布をとることがわかっています。
例えばある国のGDPや個人の収入、川を流れる小石の大きさの分布などは、様々な要因がお互いに強く影響しあっていて、特に”バタフライ効果”に説明されるように初期の分岐から何度も分岐を重ねて最終的に大きな差が出るような歴史的経過を辿っています。こういった事象は、乗算過程による対数正規分布の代表例です。
例えば日本の世帯所得は以下の厚労省のページから確認できるように、対数正規分布の形状をしています。
また意外かもしれませんが、大人の体重も対数正規分布をとることが知られています。
一様分布
最後に、最もシンプルな分布を紹介します。
上でサイコロの事例で中心極限定理を説明し、サイコロをたくさん振った時の目の平均値が正規分布するという話をしましたが、一方で”1回だけサイコロを振った時のサイコロの目”の分布は、1~6まで同じ確率で出るはずなので、すべて1/6(約17%)ずつです。このように、すべての場合で同じ確率となるような分布を一様分布と呼びます。
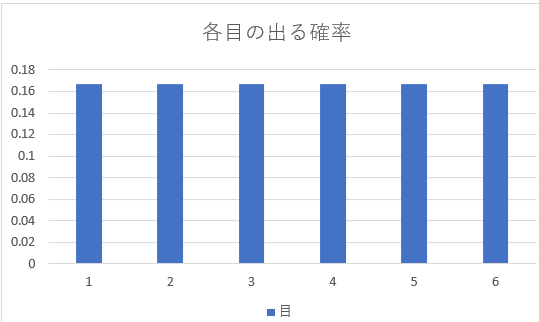
コインの表裏も同様に、1/2の一様分布です。


コメント