前回はCNN(畳み込みニューラルネットワーク)が必要とされる背景として、DNNのデメリットを解説しました。今回は、そもそも畳み込みとは何なのかを解説します。前回記事は以下を参照ください。
畳み込み(Convolution)とは何か
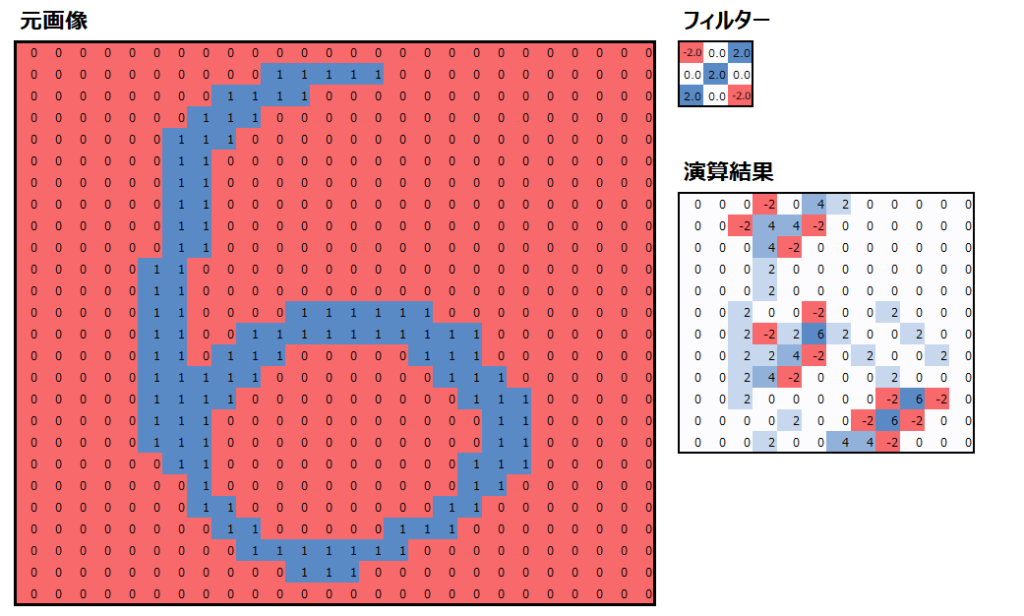
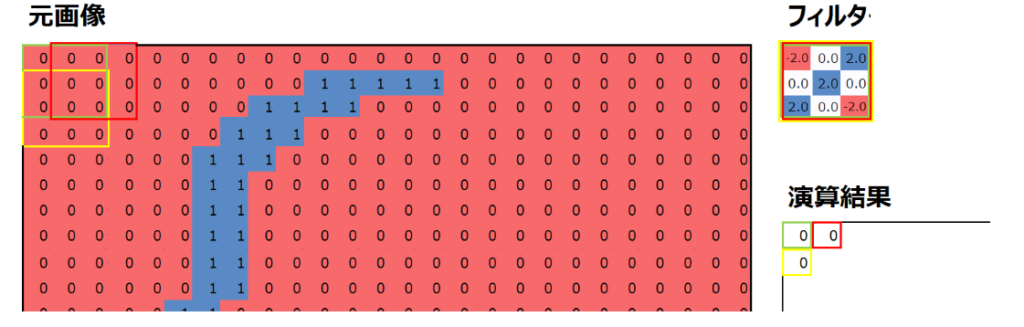
畳み込みという言葉は数学の分野において、ある関数を並行移動しながら別の関数に重ねて足し合わせることを言います。ディープラーニングにおいては以下のように、フィルターというものを用意して、元画像を平行移動しながらフィルターと掛け合わせて演算することを言います。演算の詳細は後述しますが、以下はカーネルサイズ=3×3、フィルターサイズ=1、ストライド=2の畳み込み演算の結果です。
なお、数字の羅列では見にくいので、以下の画像はカラースケールを設定し、大きい値は青字、小さい値は赤字になる様にしています。
畳み込み演算のイメージ図
では、畳み込み演算のイメージを解説していきます。まずは元画像の左上の3×3の9つの数値と、あらかじめ用意したフィルターの値について、同じ位置にある値を掛けて、それらを足し合わせます。

この作業を、元画像の位置を変えながら実行していきます。例えば元画像の位置を1列右にずらした畳み込み演算を以下の赤枠で示しています。適用するフィルター(の値)は変わらないことに注意してください。

同様に、元画像の位置を1行下にずらした畳み込み演算を以下の黄枠で示しています。

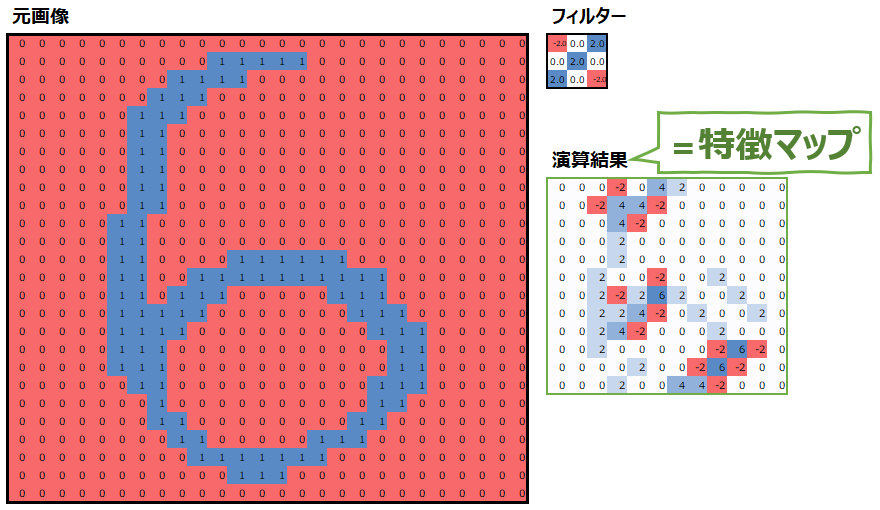
このように畳み込み演算をくり返して、演算結果を記録していって完成するものを、特徴マップと呼びます。(なぜ特徴マップというのかは後述。)
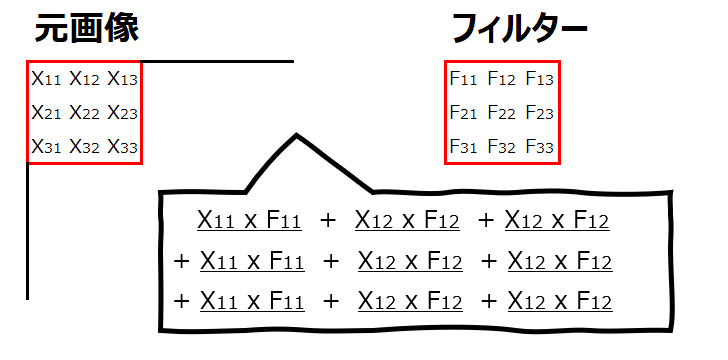
なお、同じ位置にある値を掛けて足すというのがイメージしにくいと思いますが、具体的には以下の画像の、添え字(アルファベットの右下の小さな数字)が同じもの同士を掛けて足します。
より具体的に、計算結果の例を見てみましょう。畳み込み演算の結果である特徴マップで最も値大きかったのは、以下の黄色枠の部分で、値は6です。この部分の計算プロセスを以下に示していますので、参考にしてください。

畳み込み演算の意味
上では畳み込み演算の中身について説明しました。ではこの畳み込み演算の”意味”はどう解釈することができるでしょうか。
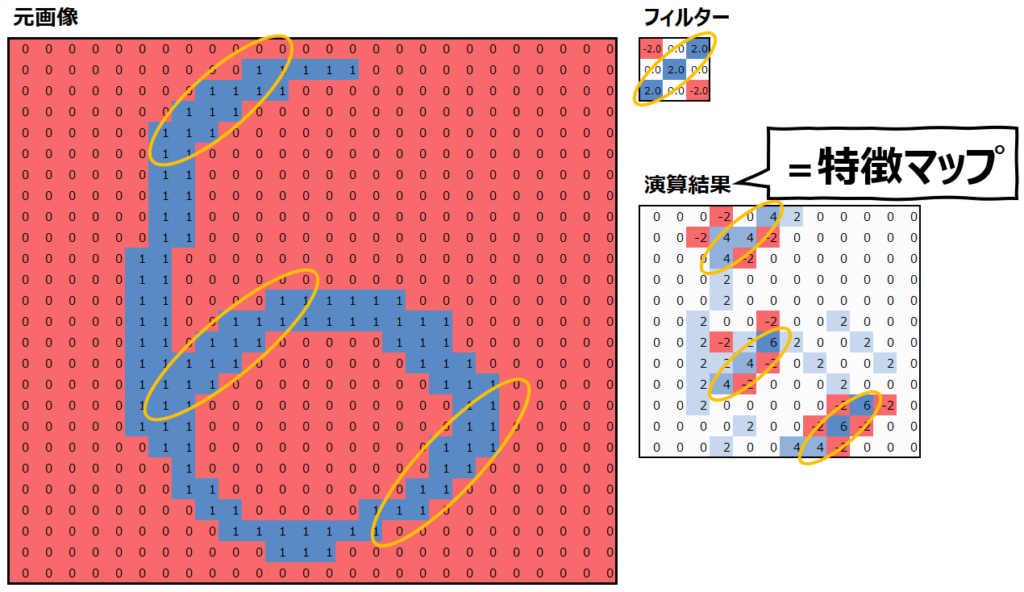
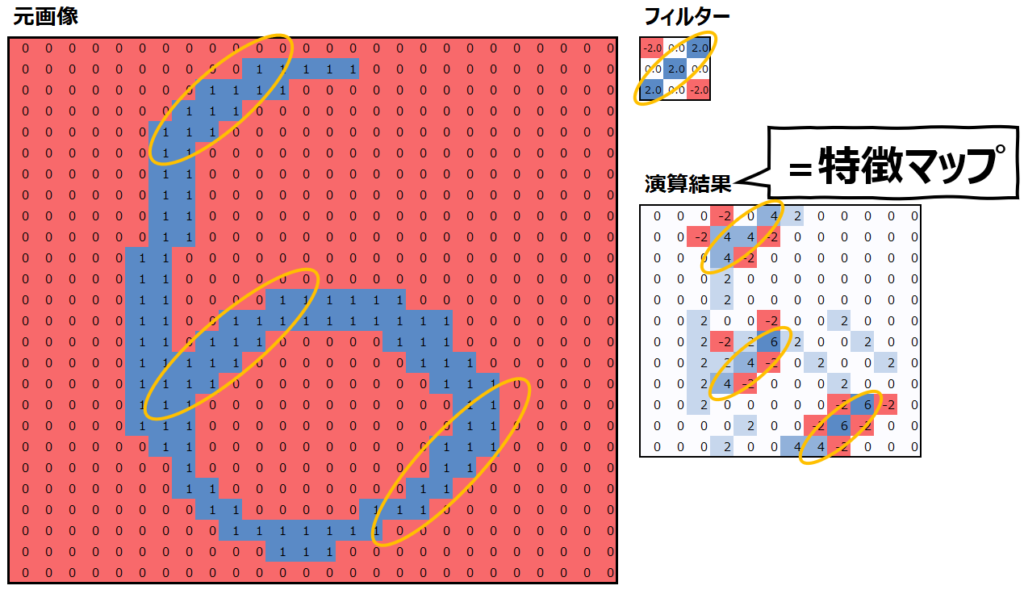
まず、上述のフィルターと特徴マップを再度見てみましょう。
この特徴マップは、“元画像とフィルターが似ているほど、特徴マップの値は大きくなる”という特性があります。似ているというのは、フィルターで値が大きい部分は元画像でも値が大きく、フィルターで値が小さい部分は元画像でも値が小さいということです。元画像の重要な特徴を抽出して表現しているので、”特徴マップ”と呼ぶのです。
実際、このフィルターは右上から左下にかけて斜めのラインで値が大きくなっていて、左上と右下は値が小さくなっています。元画像でも同様に、右上から左下にかけての斜めの部分で”1″が多く、左上と右下には”0″が多くなっていることがわかります。そして、それらの値の大小が一致している場合に、特徴マップの値が大きくなっていることがわかると思います。
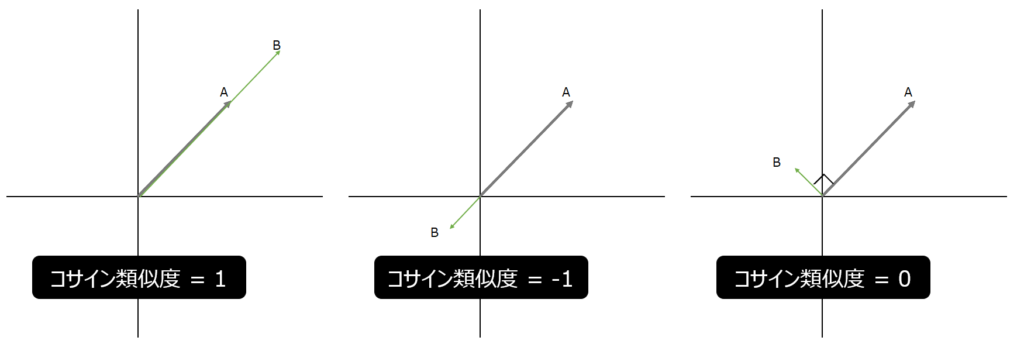
なぜこのような結果になるのか納得したい場合は、数学におけるコサイン類似度を想像してもらえればいいと思います。コサイン類似度を一言で言うと、”似ている具合”を表す指標です。直感的に説明するなら、2つのベクトルがあったときに、同じ方向を向いている時は最もよく似ているので”1″、逆行している場合は最も似ていないので”-1″、直行している場合は最もニュートラルなので”0″となります。
なお、コサイン類似度は内積という、ベクトルや行列の成分同士を掛け算によって計算されます。上での畳み込み演算も、2つの3×3の行列の成分を掛け算していることからも、コサイン類似度と特徴マップの値を関連付けやすいのではないでしょうか。
フィルターの重要性
結果的に、元画像とフィルターが似ているほど、特徴マップ上で大きな値として現れることになります。ここから言えるのは、畳み込みというのは”元画像とフィルターに共通する特徴を抽出する”ということです。上の例では、斜めの線を抽出するフィルターを用意したので、特徴マップにも、”斜め線がどこらへんにあるのか”が表現されています。
そして、フィルターを変えれば、抽出される特徴も異なります。以下の例では、まっすぐな線を抽出しています。
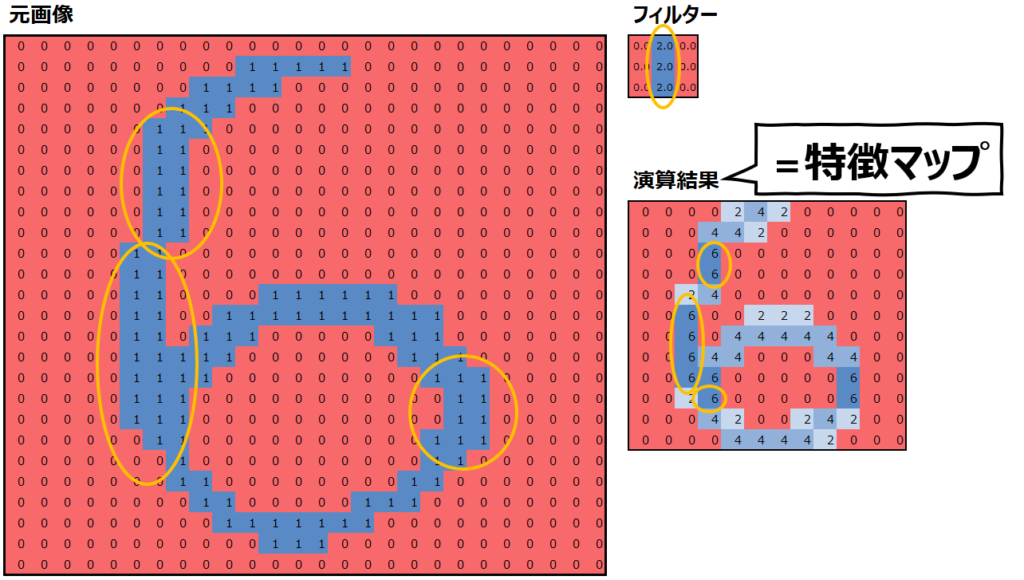
このように、畳み込みではフィルターを用意して元画像の特徴を抽出するため、このフィルターの値が極めて重要です。CNNにおいて”機械学習”が学習するのも、このフィルターの値をどう設定するか、ということになります。(ただし、学習された後の最適なフィルターの値を上述の様に直感的に理解できるとは限らない。)
カラー画像の場合(3次元データの畳み込み)
上では白黒画像を前提に話を進めました。ではカラー画像の場合はどうなるでしょうか?再度、ネズミのキャラクターに登場してもらいましょう。
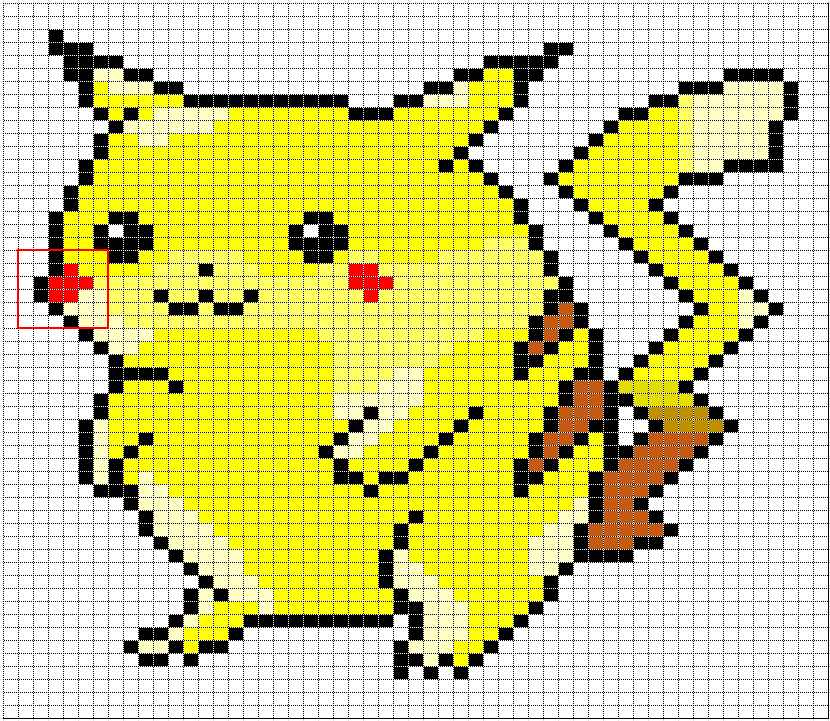
あるセルの色を表現するとき、白黒であれば1/0や、グレースケールなら0-255で表現できますが、フルカラーであればRGBの(0,0,0)~(255,255,255)の形式になります。RGBというのは、Red(赤)、Green(緑)、Blue(青)という、光の三原色の大きさで1つの色を表現する方法です。直感と反すると思いますが、最も値の大きいRGB(255,255,255)が”白”、最も値の小さいRGB(0,0,0)が”黒”に相当します。”大きい方が色が濃くなるんじゃないの?”という人間の感覚は”色の三原色”によるものと思われます。色の三原色というのはC(シアン)、M(マゼンタ)、Y(イエロー)です。詳しくは以下を参照ください。

ネズミの場合は、画像の色をRGBで分解すると以下のようになります。

例えばB(青)の値を見てみると、以下のようになっています。青画像で”青っぽく”見えている部分はBの値が大きく(255)、”黒っぽく”見えている部分はBの値が小さい(0)ことがわかります。
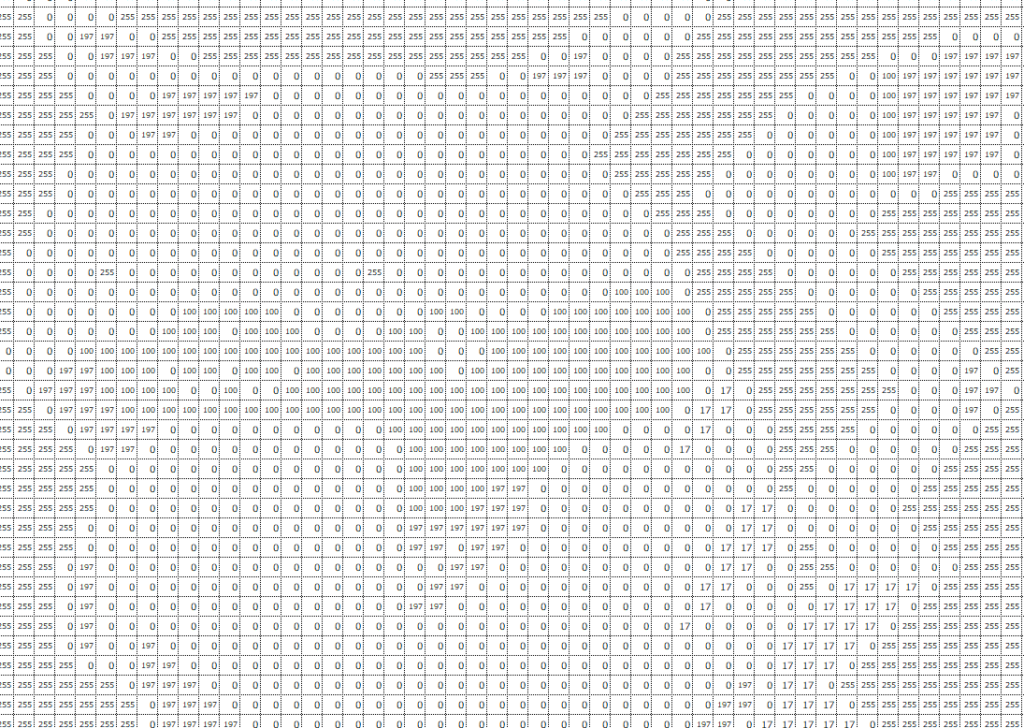
では、フルカラー画像の場合以下の赤枠の部分のRGBでの入力データはどのようになるでしょうか。

RGBのそれぞれの値は以下のようになっています。
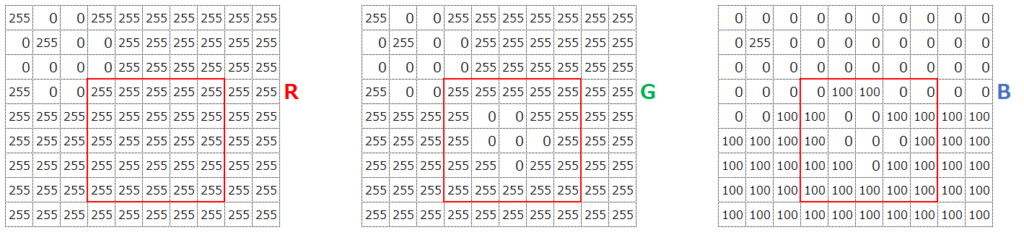
見た目に”黄色”っぽい部分は、R(赤っぽさ)とG(緑っぽさ)が最大値、B(青っぽさ)は小さい(0~100)ことがわかります。これをRGB値で表すと、あるセルの入力データは例えば(255,255,100)といった感じになります。
また中心の”赤”っぽい部分は、R(赤っぽさ)とが最大値、G(緑っぽさ)とB(青っぽさ)は最小値(0)であることがわかります。これをRGB値で表すと、あるセルの入力データは例えば(255,0,0)といった感じになります。
カラー画像の場合は、これらRGBの3つの値をそれぞれ入力データとして取り込みます。これを、チャネルが3つある、と表現します。例えば、以下の赤枠の右上のデータであれば、(R,G,B)という順で、(255,255,0)が入力データになります。
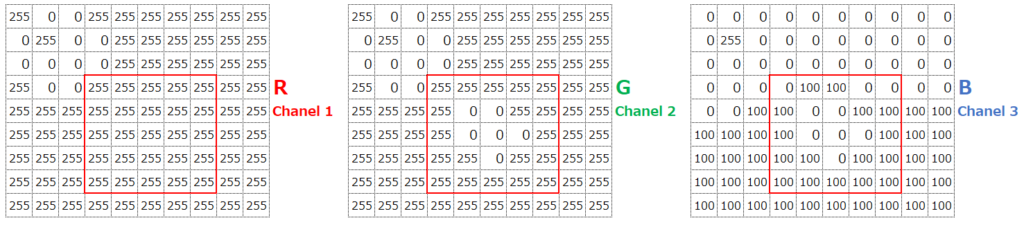
そしてカラー画像の場合、各チャネルに対してフィルターを用意します。例えば、各チャネルに対してフィルターを1つずつ用意して(フィルターサイズ=1、カーネルサイズ3×3, ストライド=2)、それらを足し合わせます。
これだと想像するのが難しいと思うので、まずはネズミのキャラクターの右耳を検知するためのフィルターを用意してみます。

例えばRGBのR値は以下のようになっています。
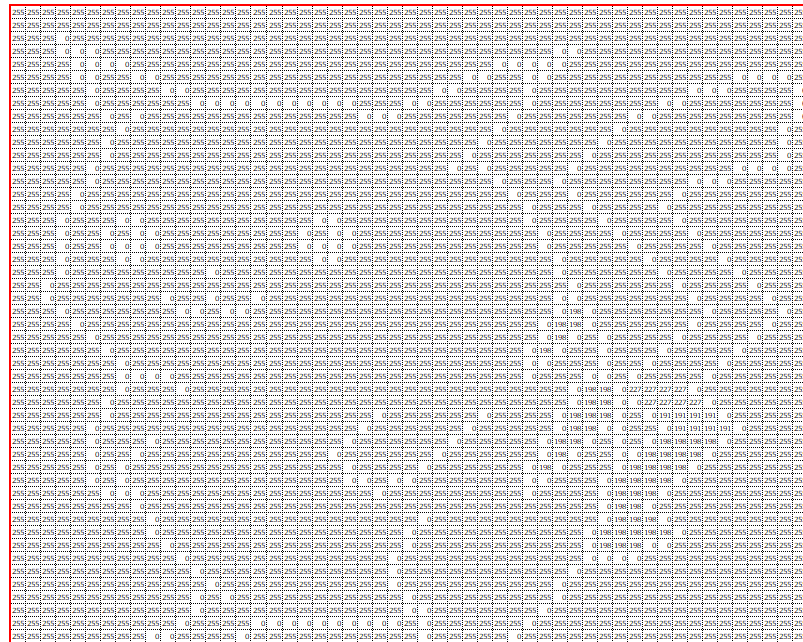
以下の図は、このR値から右耳を検知するためのフィルターを用意して畳み込み処理を実行し、特徴マップを得たものです。
例えばフィルターと元画像の左上9マスを畳み込みすると、特徴マップの左上の値が算出されています。

同じように、G値に対してG用のフィルターを使って畳み込み処理を行います。
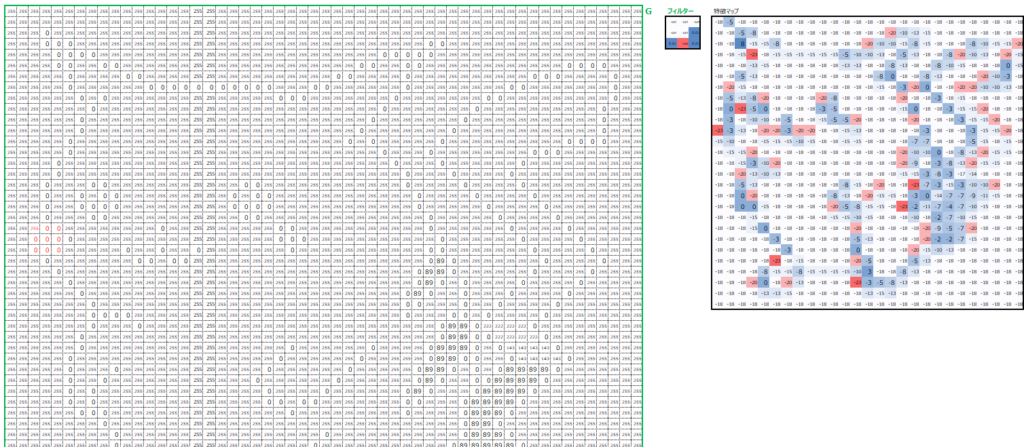
同じように、B値に対してB用のフィルターを使って畳み込み処理を行います。
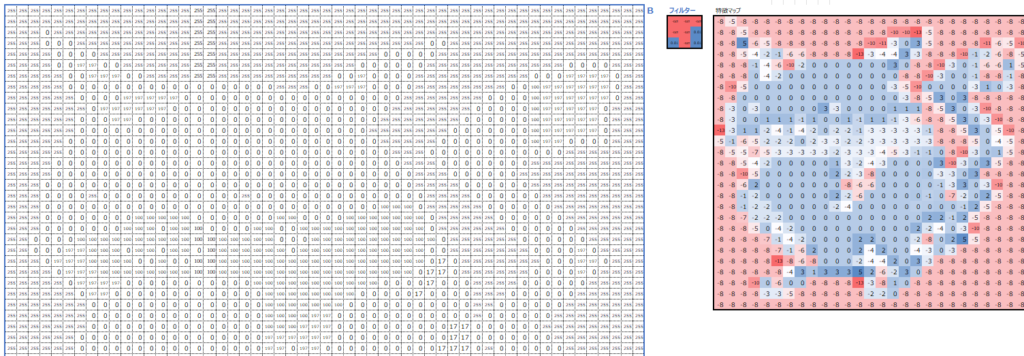
最後に、畳み込み処理の結果のRGB3つの特徴マップの値を足し合わせます。
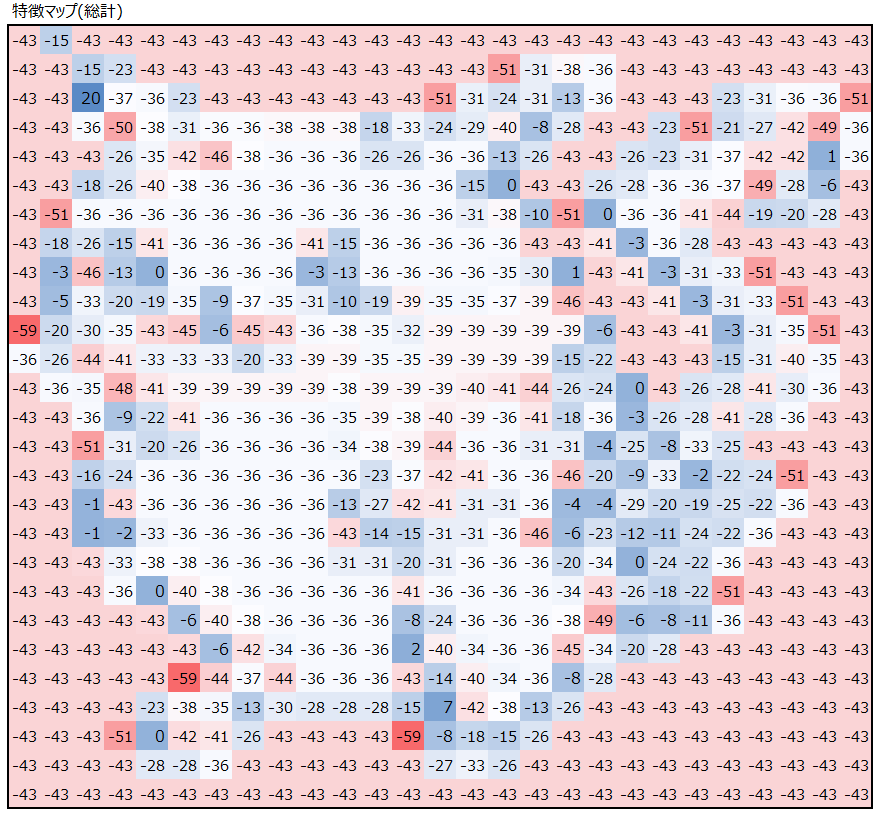
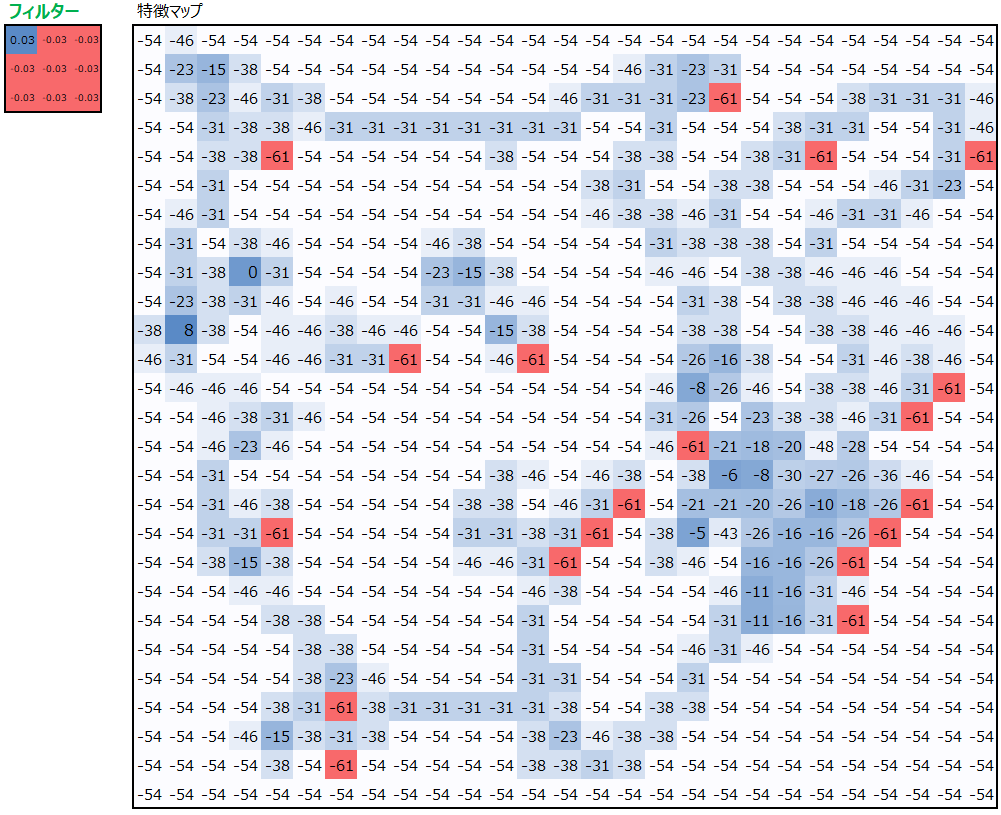
注目してほしいのは、検出したかった右耳の当りで、最も大きな値が出ていることです。
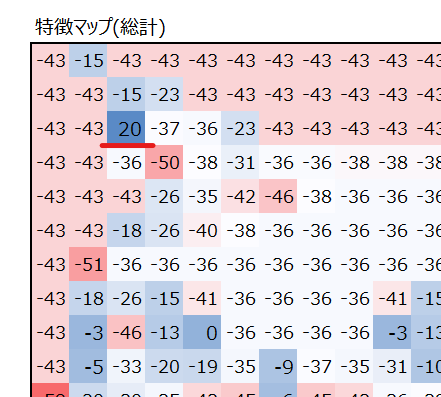
なぜ右耳の値の値が大きくなるのか、その理由はフィルターにあります。以下にフィルター3つにどのような値が設定されているかを出しています。
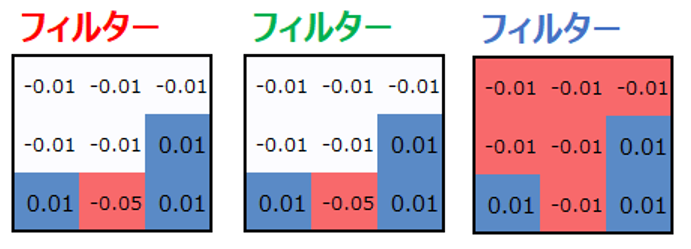
RのフィルターとGのフィルターは同じ値としていて、多くのセルにマイナス値が入っています。Bのフィルターも似た値が多いです。右耳は黒い部分が多く、黒はRGB値が”0″です。そのため、フィルターにマイナス値を入れておくと、黒から遠い色ほど畳み込みの掛け算の結果大きなマイナス値となります。黒の部分は値が0なので、マイナス値と畳み込みの掛け算をしても0のままであり、相対的に大きくなるのです。
以下を見ると、白や黄色の部分で大きなマイナス値が入っていて、黒い部分だけ小さなマイナス値もしくはプラスの値が入っていることが見て取れると思います。
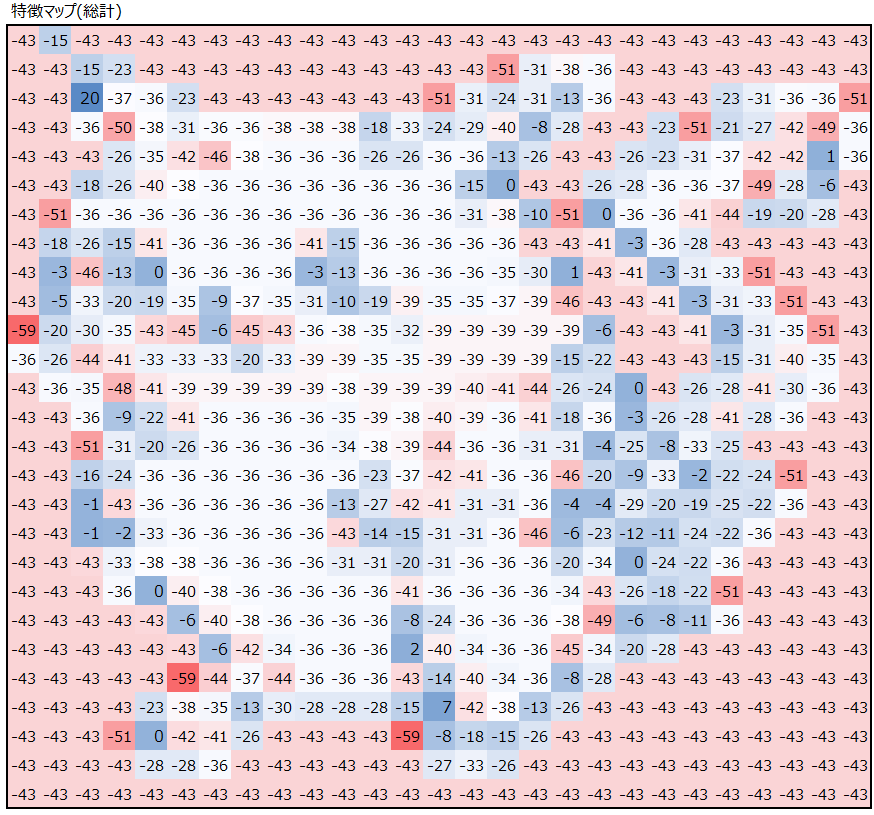
これがカラー画像の畳み込みです。
せっかくなのでもう1つフィルターを作ってみましょう。今度は以下の赤い部分を検出するフィルターを作ります。
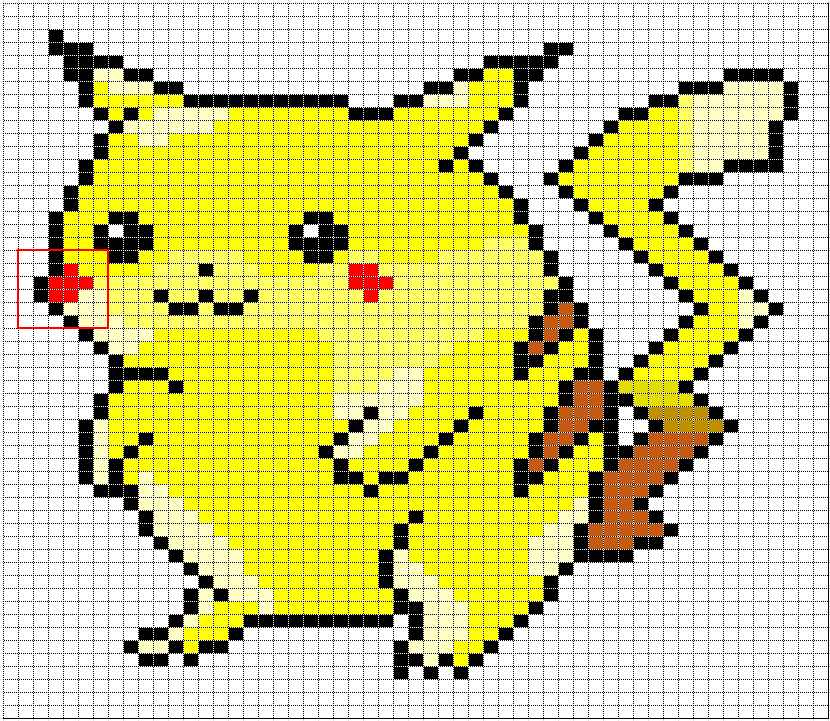
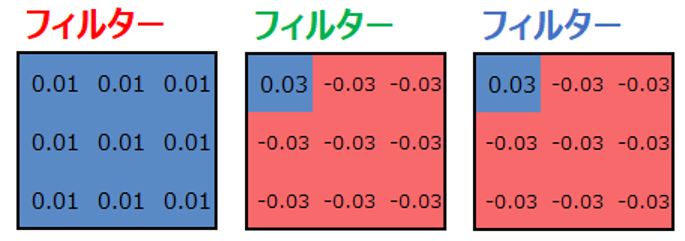
Rのフィルターを以下のように設定します。

Gのフィルターを以下のように設定します。
Bのフィルターを以下のように設定します。

最後に、畳み込み処理の結果のRGB3つの特徴マップの値を足し合わせます。狙い通り、左側の赤い部分に反応するフィルターを作ることができました。
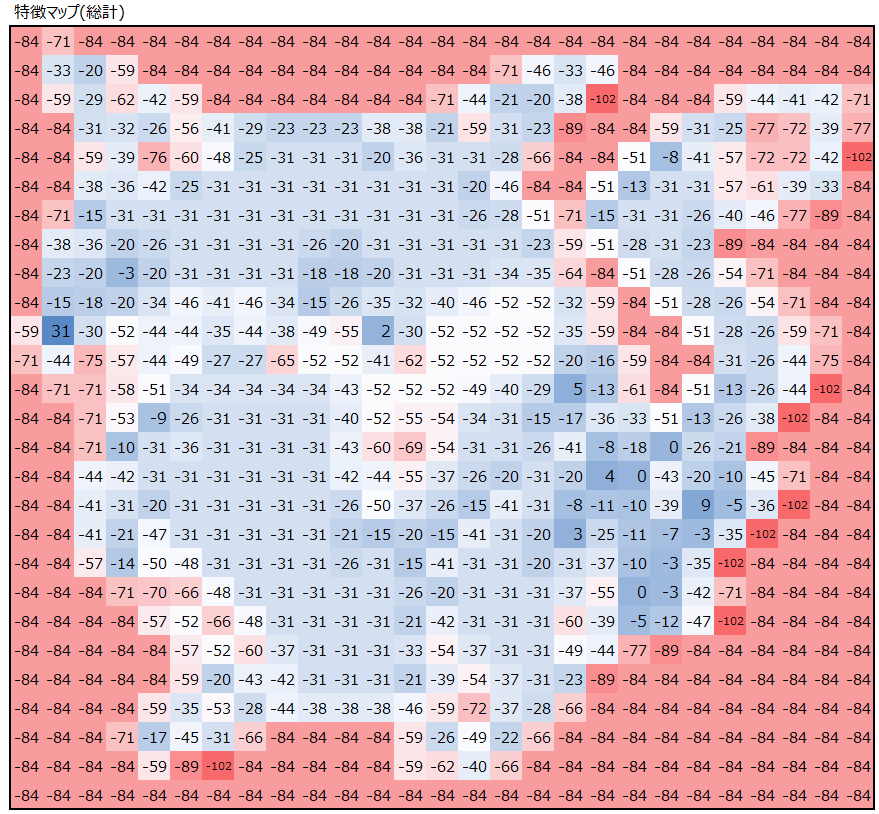
各フィルターの値は以下の通りです。検出したい部分が”真っ赤”な部分なので、Rのフィルターだけ前面がプラス値、GBは多くがマイナス値です。
畳み込みのパラメータ
さて、ここまできてようやく、畳み込みに関連するパラメータを紹介します。これを冒頭で紹介しなかったのは、上の例を頭に入れた状態の方がイメージしやすいからです。
各パラメータの解説
カーネルサイズ
1枚のフィルターの縦と横の値の数です。例えば以下のフィルターであれば3×3です。自由に設定できますが、3×3がよく使われ、他には5×5や1×1も使われます。

チャネル数
入力されるデータの次元数です。例えばカラー画像を入力する場合はRGBの3次元なので、入力層のチャネル数は3になります。

フィルターサイズ
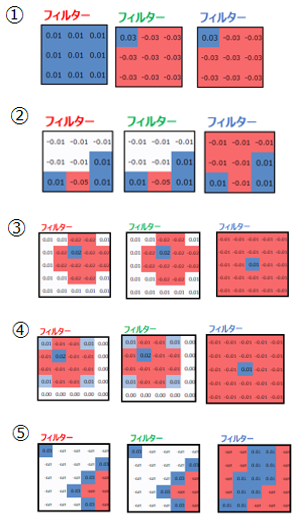
フィルターを何セット用意するか、と考えると理解しやすいと思います。例えば、以下の5種類のフィルターを用意する場合、フィルターサイズは5となります。このフィルターサイズが、出力される特徴マップの数と一致します。
①右頬の検出用
②右耳の検出用
③左目の検出用
④右目の検出用
⑤縞模様の検出用
ストライド
畳み込み演算をするときに、縦と横に何列ずれるか、というのがストライドです。以下で、ストライド1の場合とストライド2の場合の違いを図示します。
ストライド1
ストライド2

パディング
パディングは入力画像にピクセルを追加することです。今回の例では登場していませんが、重要な操作なので解説します。
畳み込みという処理はその特性上、元画像より特徴マップのサイズが小さくなります。例えば元画像5×5を入力し、3×3のフィルターを使って畳み込みをすると、出力される特徴マップは3×3となります。
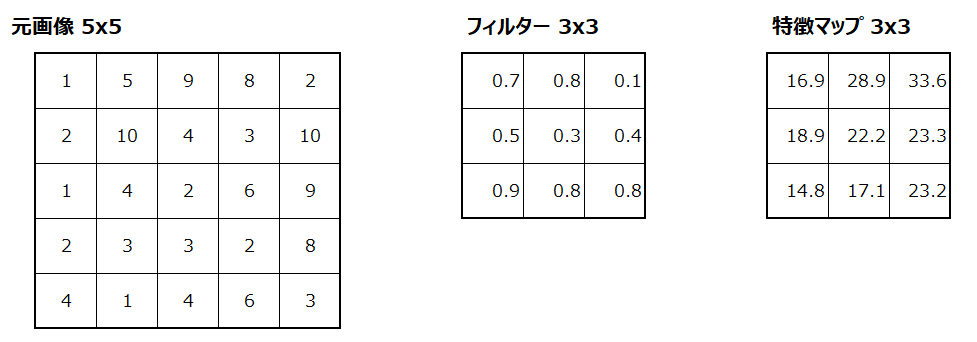
1回だけの畳み込みであればこれは特に問題になりませんが、通常CNNのモデルでは畳み込みが何度も繰り返されます。その度に出力される特徴マップが小さくなってしまうことを避けたい場合に実施するのがパディングです。具体的には以下のように、例えば元画像の周りを0で埋めることで、畳み込みを実施しても出力される特徴マップが元の入力画像と同じサイズになります。
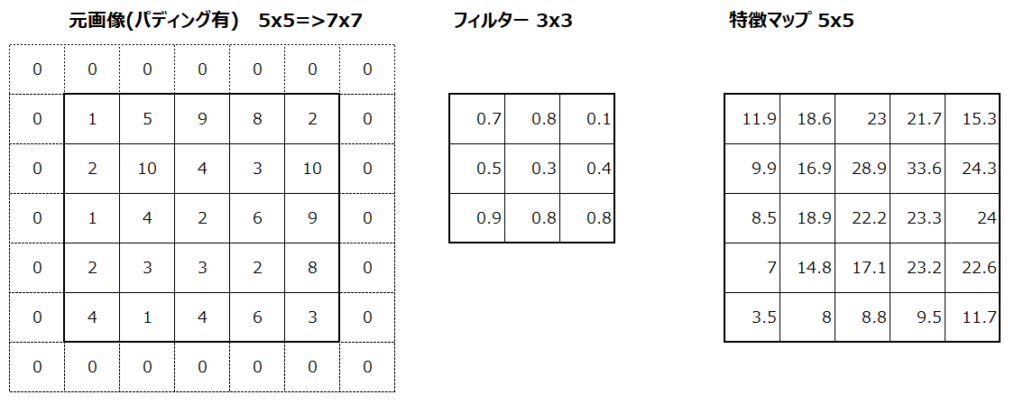
パディングの効果は特徴マップが小さくなることを防ぐというだけでなく、元画像の端の情報が失われるのを防ぐ効果もあります。
パラメータの実例
ここまで、カーネルサイズ、チャネル数、フィルターサイズ、ストライドについて説明しました。これらをネズミのキャラクターの検出にあてはめると以下のようになります。
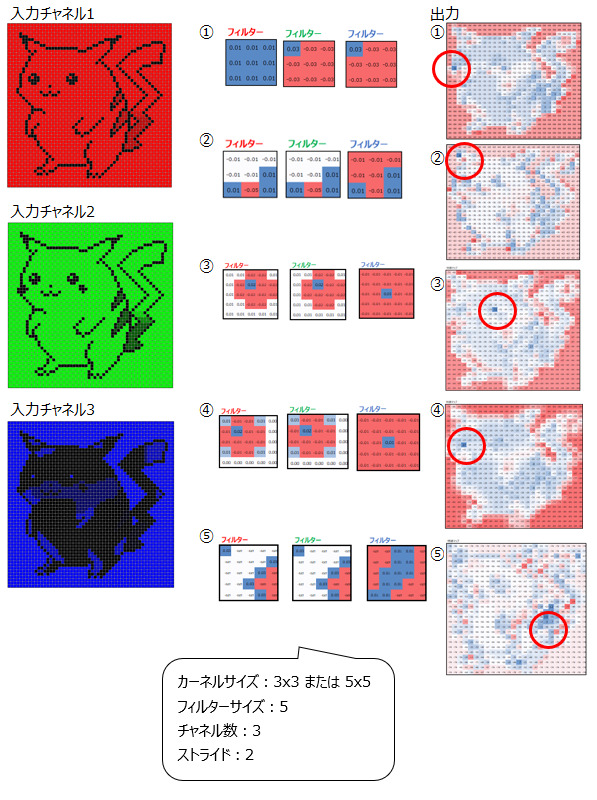
では次に、上で得られた5つの出力を次のステップの入力として、更に畳み込み処理をしてみます。
上の処理で①~⑤の特徴検出器を用いましたが、それらをいい感じのバランスで調合することで、ネズミの特徴を最大限共存させてみました。(各フィルター①~⑤の畳み込み結果は省略し、その総計だけを掲載しています。)
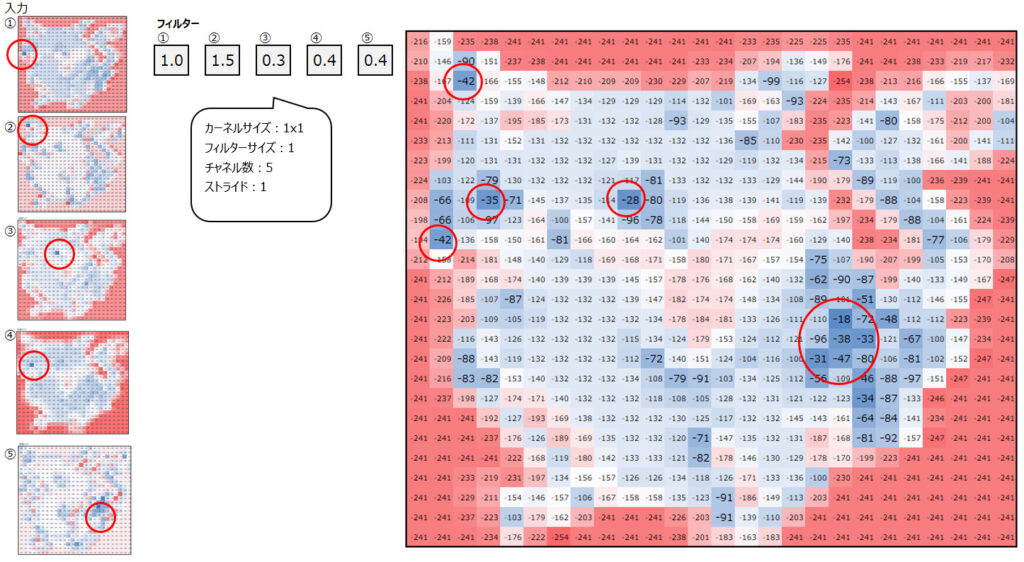
これが、畳み込みのイメージです。次の記事では、様々な畳み込みの種類を解説します。少々お待ちください。
コメント