今回は機械学習の中の教師あり学習の分野における、SVM(サポートベクターマシン)について解説します。機械学習の概要や基本的な用語の説明については以下の記事を参照ください。
SVMとは何か
SVM(Support Vector Machine, サポートベクターマシン)というのは、サポートベクトルに基づいてマージンを最大化して分類を行うアルゴリズムです。今回は以下の例を用いて説明します。以下の赤いデータと黒いデータの集合を当てはまりよく分類したい時、2つのデータの集合に距離がありますから、その間に線を引いて分類すればいいのではないか、というのが誰しも思いつくことだと思います。

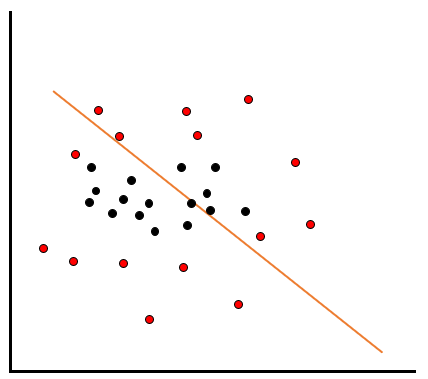
ではそういったケースで、線をどのように引くのがベストでしょうか?例えば以下のような青い線とオレンジの線の分類が考えられるとき、どちらの方がより当てはまりがいいと言えるでしょうか。

SVMでは、当てはまりの良さをサポートベクトルと分類線のマージン最大化で評価します。
サポートベクトル
サポートベクトルというのは、線を引いた時に、線から最も近いデータのことです。上の例では、以下のデータがサポートベクトルになります。
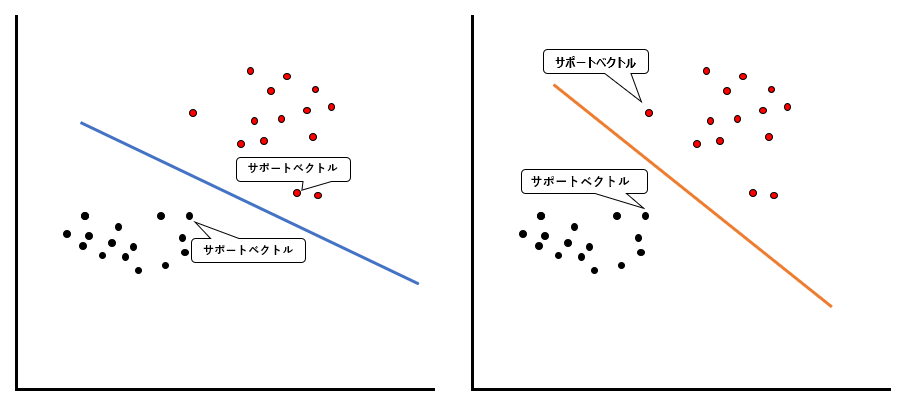
ご覧いただければわかる通り、どういった線を引くかによって、サポートベクトルとなるデータも変わります。では、このサポートベクトルと分類線のマージンを最大化するとはどういうことでしょうか。
マージン最大化
マージンを最大化するために、まずはサポートベクトルと分類線の距離(差=マージン)を測ります。青い線では黒データのサポートベクトルとの距離が5、赤データのサポートベクトルとの距離が3です。一方オレンジの線では黒データのサポートベクトルとの距離が6、赤データのサポートベクトルとの距離が4です。

この結果はつまり、青い線の方がマージンが小さい、言い換えると、サポートベクトルと青い線が接近してしまっていると言えます。接近しているということは、そのデータが少し動いてしまったら誤分類が発生するような線を引いているということです。逆にオレンジの線の方がマージンが大きく、直感的に表現するならゆとりのある線を引くことができています。
結果的に、SVMではオレンジの線の方が分類線として当てはまりが良いと評価します。
ソフトマージン法
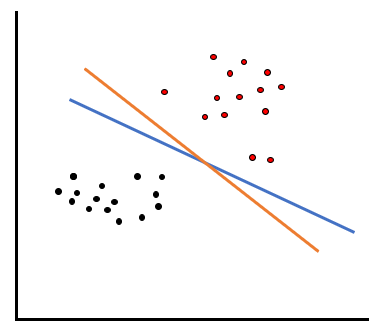
上の例では、線を引いて分類することができる、つまり線形分離が可能なケースでした。しかし、例えば以下のように赤いデータと黒いデータが混在している場合はどうでしょうか?
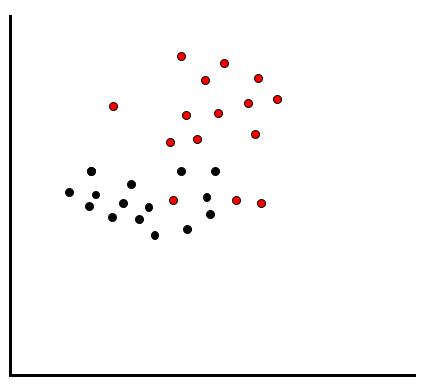
こういったケースでは、ただ線を引くだけではうまく分類することができません。例えば黒いデータを綺麗に分類しようとすると、以下のように赤いデータのエリアに黒いデータが多く入ってしまいます。
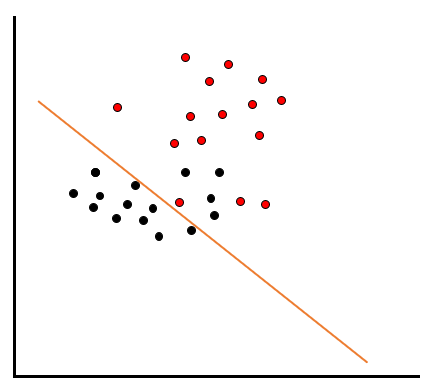
反対に赤いデータを綺麗に分類しようとすると、以下のように黒いデータのエリアに赤いデータが多く入ってしまいます。

こういったケースで使うのが、SVMのソフトマージン法です。ソフトマージンを直感的に説明するならば、上記で説明したマージン最大化を、ソフトに、ゆるく適用する方法です。なお、線形分離が可能な場合のSVMをハードマージン法と呼びます。
具体的には、線形分離不可能な場合にスラッグ変数ξ(クサイ)を導入して、線形を一定の距離距離ずらした場合に変数ξの範囲内に入れば良いという評価を行いながら、マージンが最大化するような最適な分類線を探します。
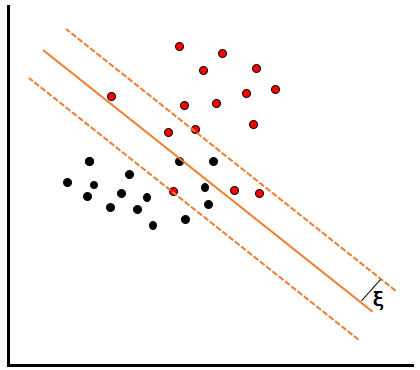
例えば上のように、オレンジの実践のように線を引いただけでは黒と赤のデータが混在していますが、変数ξの点線の範囲内であればすべてのデータを綺麗に分けることができます。これが、ソフトマージン法です。
カーネル法
もう1つ、線形分離が不可能なケースで用いられるの手法としてカーネル法を紹介します。今度は以下のようにデータが散在しているケースを想定してください。
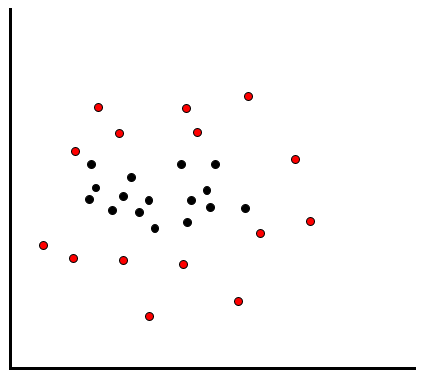
こういった分布をしていると、どのように線を引いても、赤と黒を綺麗に分類することはできません。
こういったときに使われるのがカーネル法です。カーネル法では、敢えてデータを高次元化させることで綺麗な分類を試みます。例えば2次元のデータに、X軸やY軸の3次元目のデータを加えることで、線形分離可能にします。

上図の右側では、グレーの面で分離することができています。これがカーネル法の直感的な説明です。


コメント