今回は、相関とは何か、相関係数とは何かについて解説します。
相関とは何か
相関というのは、2つの事柄の関係性において相関係数の値が正負どちらかで大きいもののことを指します。過去に”因果関係と相関関係の違い”に関する記事を書いています。そもそも相関というのがどういう状態なのかをイメージできていない方は、先にこちらをお読みください。直感的に理解できるはずです。
では相関係数とは何でしょうか。以下に解説します。
相関係数とは何か
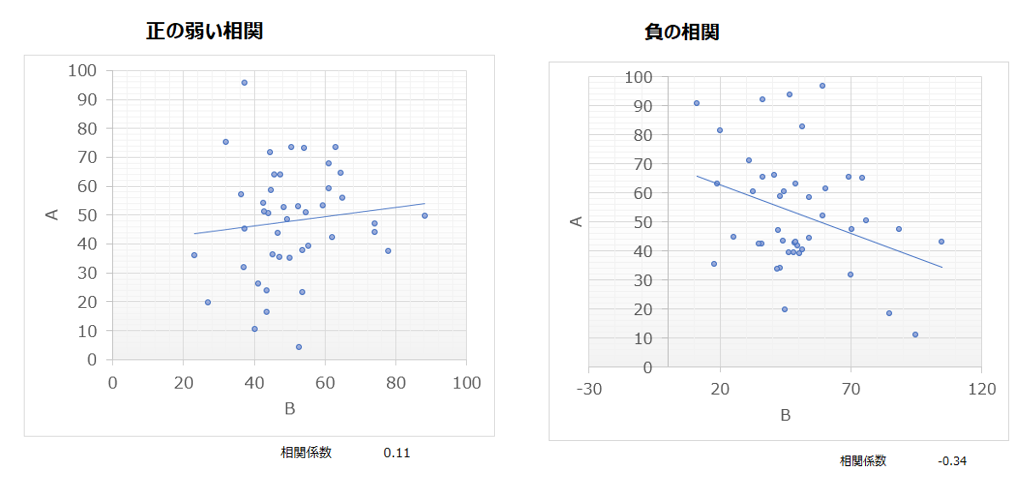
相関係数は、2つの変数間の関係の方向と強さを表す統計的な尺度です。”r”という記号で表され、範囲は-1~+1です。
相関係数が+1の場合は、完全な正の相関を示し、一方の変数が増加すると、もう一方の変数も直線的に増加することを意味します。相関係数-1は完全な負の相関を示し、一方の変数が増加すると、他方の変数が直線的に減少することを意味します。相関係数が0であれば、2つの変数に相関がないことを意味します。
計算方法
相関係数は以下の通り算出されます。
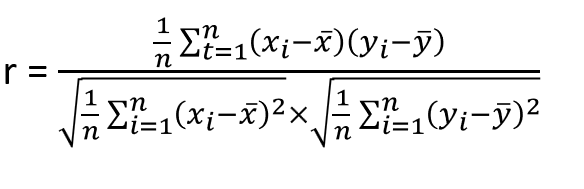
この式だと難しすぎて理解する気にならないと思いますので、直感的な説明の式に直します。

ここからわかる通り、相関係数の計算式は、2つの変数間の共分散を計算し、それを2つの標準偏差の積で割るというものです。では分散・標準偏差・共分散とは何でしょうか?
分散、標準偏差、共分散とは何か
分散、標準偏差、共分散はいずれも、データがどの程度広がっているか、2つのデータの塊がどの程度関連しているかを理解するのに役立つ統計用語です。
分散
分散は、あるデータセットに含まれる個々の値が、平均値からどの程度ばらついているかを示す尺度です。平均値から各値を引いた値を偏差と呼びますが、その偏差を二乗し、二乗した差の平均を取ることで算出されます。
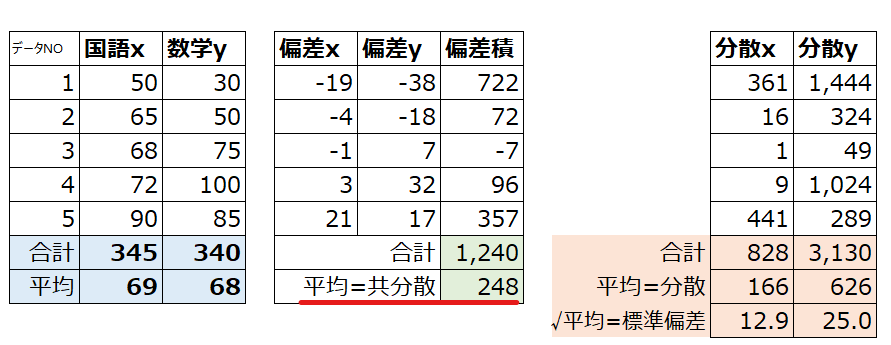
以下の例では、xである国語の点数の分散が166、yである数学の点数の分散が626です。

分散が大きいとデータがより広がっていることを意味し、小さいとデータが平均の周りに緊密に集まっていることを意味しますので、上の例では、国語と数学は平均点はほぼ同じですが、数学の方が分散が大きく、データがより広がっていることがわかります。
標準偏差
標準偏差は、あるデータの値が平均値からどの程度ばらつくかを示す尺度で、分散の平方根を取ることによって計算されます。分散と同じく、標準偏差が小さいほど、データが平均の周りに密集していることを意味し、一方、標準偏差が大きいほど、データがより広がっていることを意味します。
先ほどの例を使いまわすと、xである国語の点数の標準偏差が12.9、yである数学の点数の分散が25.0です。

分散と標準偏差
分散も標準偏差も、データが平均値からどの程度ばらついているかを示す尺度です。しかし、標準偏差の方が理解しやすく使いやすいので、より一般的に使われています。
この2つの尺度の大きな違いは、分散が2乗の単位で表されるのに対し、標準偏差は元のデータと同じ単位で表されることです。上の例では、国語と数学の点数の分散は、平均からの点数の差(偏差)の2乗の値を使っているので、元々の点数のデータと単位がずれてしまっています。
一方標準偏差は、2乗値で計算された分散の平方根を取るので、元のデータと同じ単位に戻っています。このため、理解しやすく、他の人に伝えるのも簡単です。分散よりも直感的で扱いやすいということです。
例えば、ある作業を完了するのにかかる時間を測定しているとき、標準偏差が5分だったとします。これは、平均の作業時間からの平均的なばらつき具合が5分であることを表しますが、これはその2乗値である“25”という分散よりもはるかに簡単に解釈することができます。
まとめると、分散と標準偏差はどちらもデータが平均からどれくらい異なるかを示す指標ですが、標準偏差は元のデータと同じ単位で表され、より直感的で扱いやすいため、より一般的に使用されています。
共分散
共分散は、2つの変数が一緒に変化するかどうかを示す尺度である。2つの変数が同時に増えたり減ったりするような場合を正の共分散、逆の動きをする場合を負の共分散と呼びます。
2つの変数間の共分散を計算するには、相関係数の式でも出てきたように以下の式を使用します。平均からの点数の差を偏差と呼ぶと紹介しましたが、xとyの偏差を掛けた値(偏差積)について全て合計し、平均を取ります。

相関係数の意味をどう理解したらよいか?
ここまで説明した内容を踏まえて、以下のように相関係数を計算することができます。

ではこの相関係数はなぜ、2つの変数間の直線関係の強さと方向を示し、その範囲は-1.0~1.0で、-1.0は完全に負の相関、0は相関なし、1.0は完全に正の相関を表すのでしょうか?その理由は一言で言えば、相関係数というのが一種の正規化だからです。相関係数を計算するとき、共分散を2つの変数の標準偏差の積で割りますが、これは共分散を正規化し、2つの変数のスケールを考慮しているといえます。
では、正規化について説明します。2つの変数の間の共分散を計算するとき、結果の値はそれぞれの変数に使われる測定単位に影響されます。例えば、テストの点数が10点満点と100点満点の時では、共分散の値も10倍異なります。また例えば、国語のテストを100点満点で測定し、数学を150点満点で測定した場合、共分散は両方の変数が100点満点で測定された場合とは異なってしまいます。これでは指標として共分散が使いにくいので、共分散をxとyの標準偏差の積で割ることで、共分散を、2つの変数の尺度を考慮した値にすることができます。こういった操作のことを正規化と呼びます。
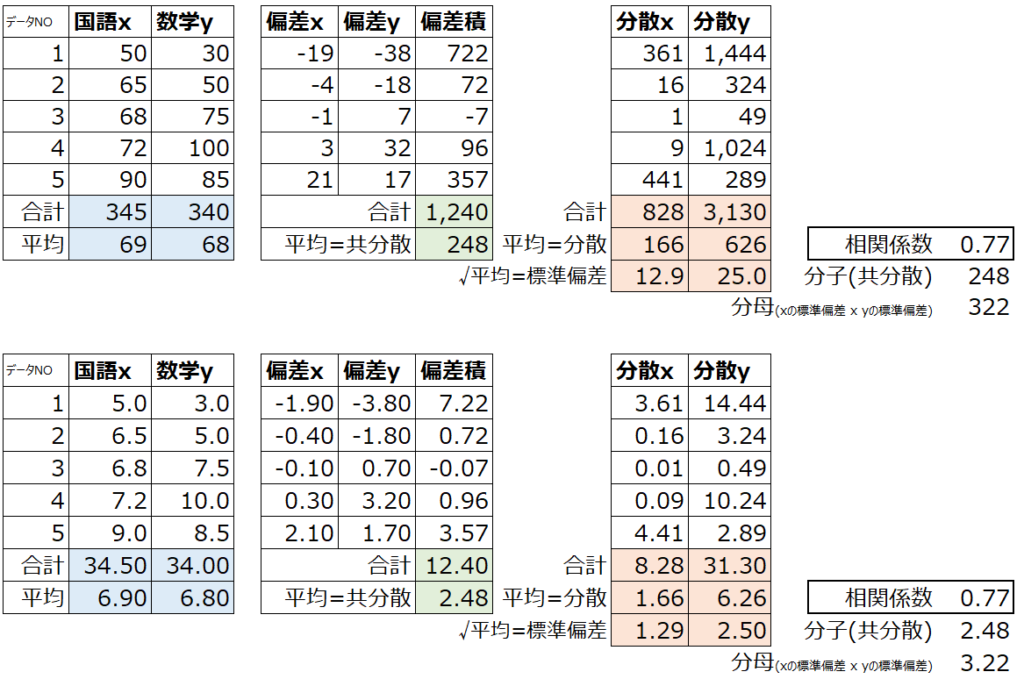
以下では、実際に点数を100点満点と10点満点の時で比べています。共分散は10倍異なりますが、相関係数は同じであることがわかります。
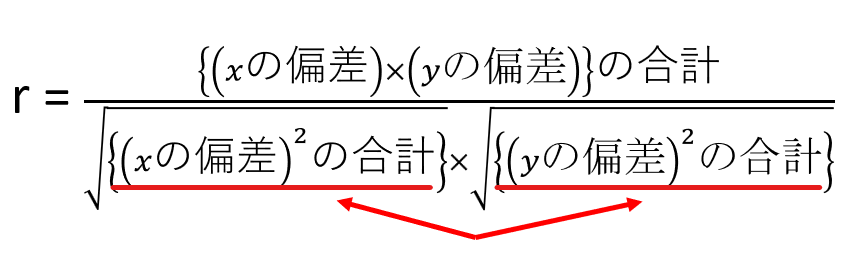
では正規化すると、なぜ-1~+1の範囲の指標になるのでしょうか。それを直感的に理解してみましょう。以下は最初に掲載した相関係数の計算式です。
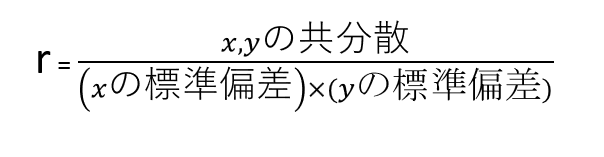
これを、以下のように書き換えてみます。そうすると、なぜ-1~+1なのかが見えやすくなります。というのも、分母と分子に似たような値があるからです。
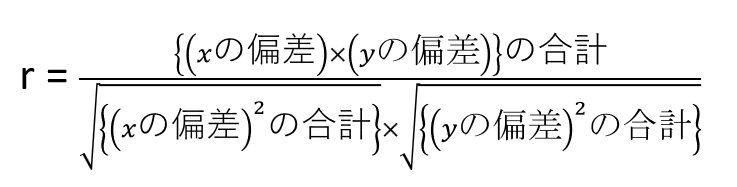
まずは、相関係数の最大値が1であることのイメージを掴みましょう。分子はxとyの偏差を掛けてから合計していますが、分母は偏差を合計してから掛けています。つまり、最大の違いは掛けてから足すか、足してから掛けるかの順番の違いです。
実際に数値を置いて、足し算と掛け算の順番が違うことでどのような違いが生まれるかを見てみましょう。以下の例では、ケース1では分子(共分散)と分母(標準偏差x標準偏差)が同じ値で、相関係数も1になります。一方ケース2では、偏差yの値は変えずに並び順だけ変えたところ、分子の共分散が小さくなり、相関係数の値も小さくなりました。
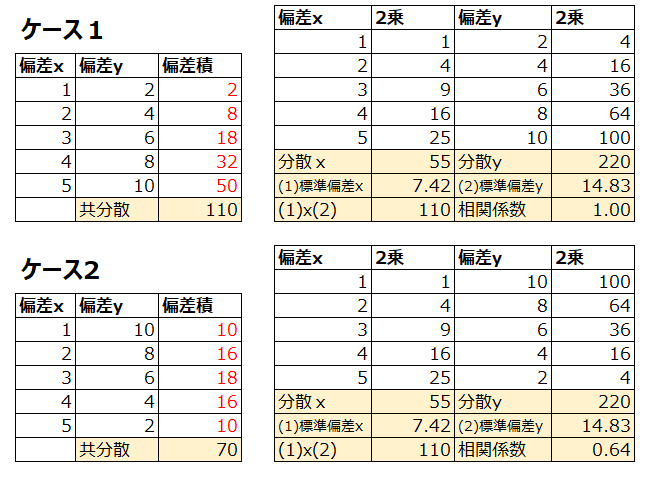
つまり、相関係数の分子と分母は同じ材料を使って計算(掛け算と足し算)しているものの、分子の共分散の様に先に掛け算してから足す場合は、大きい値同士で掛け算してから足して初めて、分母と同じ値になるようになっているのです。小学校で習った足し算と掛け算の順番の重要性を、ここにきて思い知りますね。
これが、あくまで直感的に理解のための、”なぜ相関係数の最大値は1なのか”です。
次に、最小値が-1である理由を見てみましょう。こちらは簡単です。偏差というのは上述の通り{あるデータの値-平均値}ですので、プラスにもマイナスにもなります。平均点50点のテストで、60点の人の偏差は+10ですが、40点の人の偏差は-10です。
相関係数の式を見ると、分子は偏差同士を掛け算するため、どちらかだけがマイナスの時は、分子の共分散全体がマイナスの値を取ります。一方、分母は2乗してから平方根を取っているため、必ずプラスの値とプラスの値の掛け算となり、分母全体も必ずプラスになります。
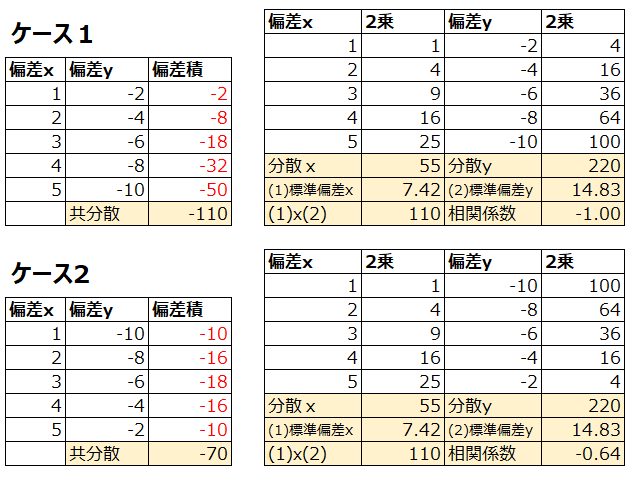
そして、最大値が+1になるような性質で、マイナスになることもあるわけですから、最小値は-1になるのです。先ほどの表の値を、相関係数がマイナスになるように書き換えました。
これで、相関係数というのが何なのか、直感的に理解できたのではないでしょうか。
相関係数のデメリット
以上紹介してきた相関係数ですが、どんな時でも使えるわけではありません。
相関係数は、直線的な相関しか見ることができません。例えば2次関数的な相関をみると、0になってしまうというデメリットがあります。
また、相関係数は身長・売上・点数のような量的変数同士の相関関係を見ることに使えますが、性別・年齢などのような質的変数同士の相関関係を見るには使うことができません。
質的変数同士を比べる際には、以下のようにクロス集計をする必要があります。この例では、ある映画について、男女別に評価を聞いた結果です。

以上紹介したように、相関係数を使えるケースと使えないケースがあることを理解しましょう。


コメント