今回は、よく混同される相関関係と因果関係の違いについて解説します。
相関関係とは何か
まずは誤解されやすい、相関関係について説明します。
相関関係というのは、2つの事象について、プラスもしくはマイナスで”相関係数が大きい”関係のことです。相関係数については以下を参照ください。
相関関係を直感的に説明するなら2つの対象に関して、片方が変化した時にもう片方も変化するような関係のことを指します。
よく見かけるのは以下のような右肩上がりの散布図でしょうか。”相関”という言葉で最もイメージしやすい図だと思います。Aが高いデータはBも高い場合が多いです(逆もしかり)。こういった関係を“正の強い相関”と呼びます。
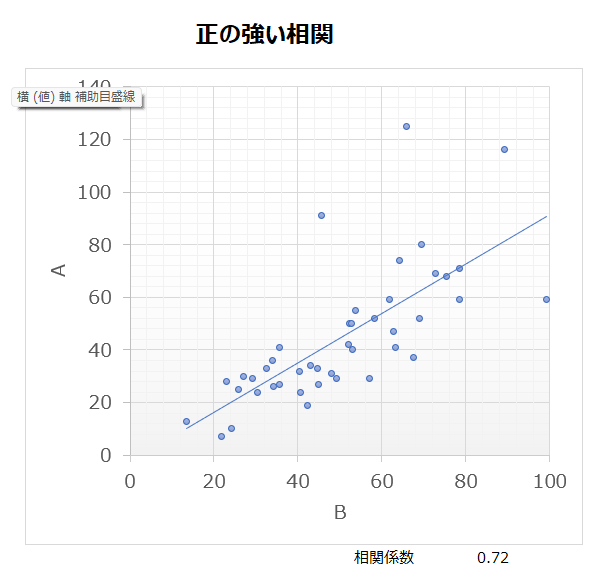
“正の強い相関”という言葉からわかる通り、相関関係には“正負”つまりプラスかマイナスかという要素と、“強弱”という要素があります。”正負”については、相関係数がプラス(右肩上がり)の関係を正の相関と呼び、マイナス(右肩下がり)の関係を負の相関と呼びます。また相関係数が1または-1に近い関係を”強い相関”、0に近い場合を”弱い相関”と呼びます。相関係数の話はまた別の機会に解説します。
“正の強い相関”以外にも、以下のような相関関係があります。
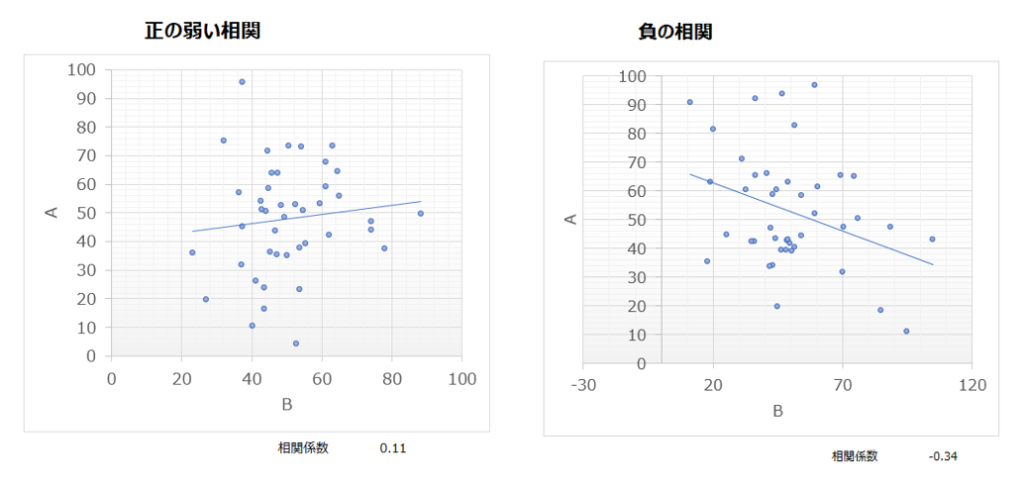
ここで気づいてほしいのは、相関というのは2つの対象についての特徴を描写している(右肩上がり等)だけであり、因果関係つまりどちらかが原因でどちらかが結果とは全く言っていないということです。
因果関係とは何か
では次に、因果関係について簡単に説明します。こちらは理解している人が多いのではないかと思いますが、因果関係というのは2つの事象について、片方が原因で、もう片方が結果である関係のことです。ここで大切なのは、因果関係においては必ず一方向の矢印が存在するということです。
敢えて身近な例で説明します。飲酒運転をしたことで警察に捕まったとしましょう。この時、原因は飲酒運転をしたことで、結果は警察に捕まったことです。矢印は以下のように、左から右に引くことができます。
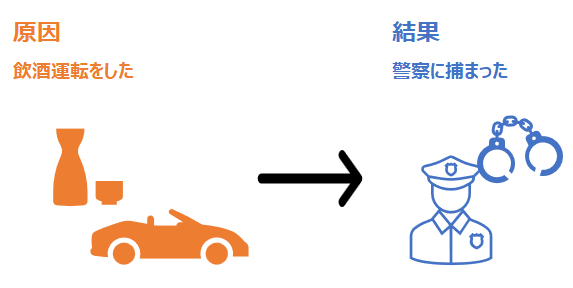
ここで、因果関係の矢印を反対にすることはできないことに注意してください。以下のように、警察に捕まったことが原因で飲酒運転をした、としたら、それは全く別のストーリーになってしまいます。(やけ酒?)

もう1つ例を出します。ここでは因果関係を2つ例示しています。ここでも、明確に矢印は一方向であり、逆にはならないことがわかると思います。
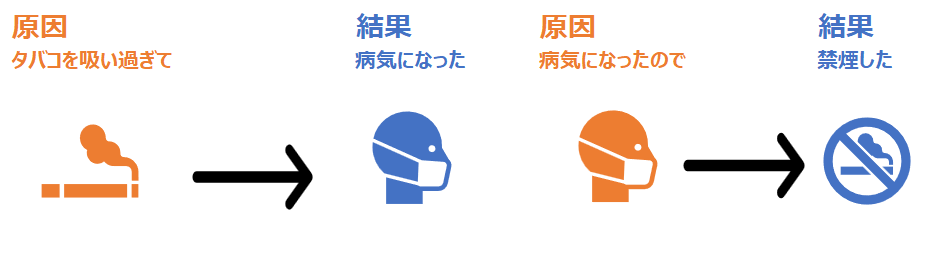
大切なことなので強調しますが、因果関係というのは、どちらが原因でどちらが結果であるかが自明でなくてはなりません。矢印は双方向ではなく、必ず一方向なのです。
両者を区別する必要性
では、なぜ相関関係と因果関係を区別する必要があるのでしょうか。
それは、世の中では相関関係を”因果関係”として誤って(又は故意に)説明されることが非常に多いからです。
例えば、以下は架空のデータで作成した散布図です。世界史の点数と数学の点数がある程度正の相関を示していることがわかります。
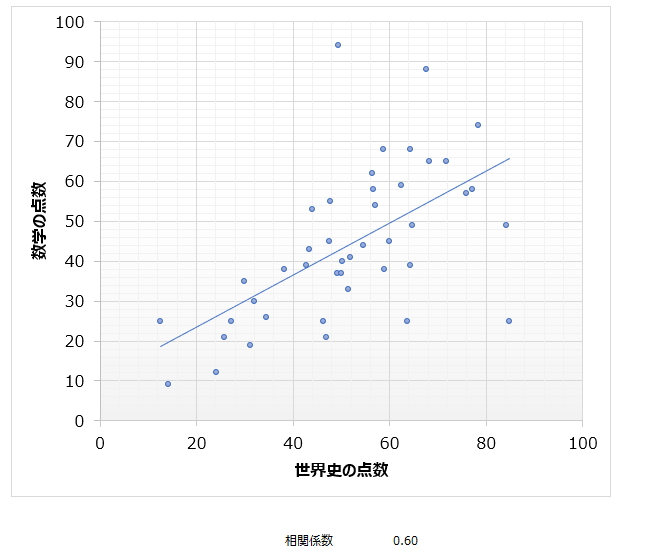
この図を見て、すぐさま因果関係と捉える人は少ないと思います。因果関係として捉えるということは、”世界史の点数が高い”ことが原因で”数学の点数も高い”という結果が得られる、もしくはその逆の矢印を引くことができるということです。
世界史の点数と数学の点数の相関が高いことの原因は様々な因子が考えられます。因果関係の可能性ももちろんありますが、”基礎学力が高い”といった別の共通因子があるかもしれないし、世界史の点数と数学の点数はそれぞれ全く別の因子と因果関係で結ばれるかもしれません。
他にも、例えば”アイスクリームの販売量と溺死者数”の相関が高かったとしても、直接の因子ではなく、”夏だから”という他の共通因子があるのではないかとすぐに想像できますね。
いずれにしても、大切なのは相関関係だけでは因果関係はわからない、ということです。
では次の例はどうでしょうか?こちらも、架空のデータです。
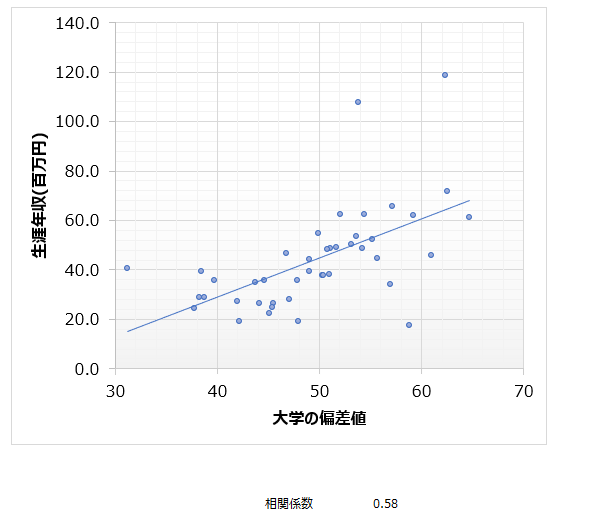
先ほどの世界史と数学の相関が必ずしも因果関係ではないということが理解できた人でも、なぜかこの例では”大学の偏差値が高い”ことが原因で、”生涯年収(百万円)も高い”ことが結果であると、一方向の矢印を引いてしまいやすいのではないでしょうか。実際にはこのデータからでは、因果関係があるかどうかは全く分からないにもかかわらず、です。
これが、両者をはっきり区別すべき理由です。もし相関関係と因果関係を混同してしまうと、散布図を見せられただけで、真実ではないかもしれない因果関係を想像するようになってしまいます。


コメント