今回は機械学習で使われるアルゴリズム決定木(decision tree)について解説します。
決定木とは何か
決定木というのは、木の構造を模したアルゴリズムです。分類問題で使われることが多いですが、回帰問題にも使うことができます。
決定木では、データの集合に対してある条件を適用して当てはまるか否かで2グループに分けるというプロセスを繰り返して、データを分類していきます。例えば以下のように、大量のメールからスパムメールを自動で判別する決定木を考えてみます。

スパムではないメールを白、スパムを黒、その混合物をグレーで表現しています。まずは大量のメールの集合に対して、”差出人はアドレス帳に登録されている”かという条件で分類します。この条件を満たすYesのものはスパムではないと見做し、Noのメールは次の枝分かれに進みます。

次に、”過去にスパム登録されたアドレス”かどうかという条件を適用し、Yesの場合はスパムであると判定し、Noの場合はさらに次の質問に向かいます。

こういったプロセスを繰り返して、すべてのメールについてスパムかどうかを判定していくのが、決定木の考え方です。
条件(線引き)の設定
上のような枝分かれによる分類を可能にする決定木は、“枝分れ前の不純度”と”枝分れ後の不純度”の差が最も大きくなるような条件を設定します。
不純度というのが何を考えるために、今度はツリー図ではなく、以下のようにグラフを使って考えてみましょう。
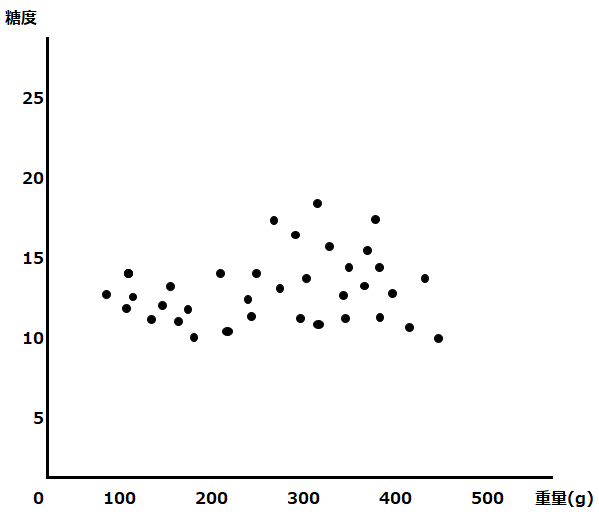
縦軸に糖度、横軸に重量のグラフ上に、果物のデータが散在しています。これらのデータは実際にはマンゴー、みかん、グレープフルーツのいずれかで、以下のように分布しているとしましょう。この状態のグラフを①とします。

オレンジ色がみかん、赤がマンゴー、黄色がグレープフルーツです。このデータを、決定木を使って分割します。まず初めの条件は”重量200g超かどうか“だとします。それをグラフ上では以下のような黒い線で表現できます。この条件(線引き)によって、みかんをすべて区別することができました。この状態のグラフを②とします。
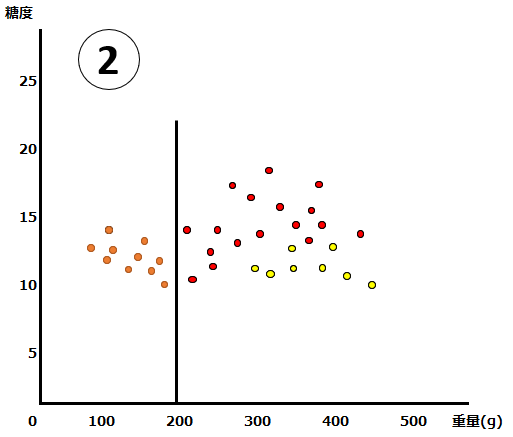
②については、みかんを綺麗に判別できているので、異論もないと思います。では次の条件(線引)は、どのように設定したら、うまく枝分かれさせることができるでしょうか?以下では、3種類の条件の設定を考えてみます。

③の条件は”糖度12超かどうか”、④の条件は”糖度14超かどうか”、そして⑤の条件は”重量280g超かどうか”です。さて、どの分け方がベストでしょうか?
決定木のアルゴリズム
決定木は上述のような問題に対し、後述する不純度の概念を用いて、以下のプロセスで学習を進めます。
- ある領域の説明変数について、その入力値と分割候補ごとの不純度をすべて計算する
- 不純度が最も小さくなる分割の方法で分割を実行
- 上記をくり返す
不純度とは何か
こういったケースで、どのくらい上手に条件(線引き)を設定できているかを測るのが、という“不純度“指標です。不純度にはいくつかの計算方法がありますが、以下では最もよく使われるジニ不純度を使います。ジニ不純度は、以下のような数式で表されますが、これだけでは意味が分からないと思うので、具体例を出して説明します。
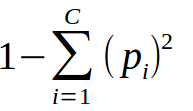
まず①の状態におけるジニ不純度を計算します。この段階では全く分類しておらず、ジニ不純度としては1-{(みかんの数/全体の数)2 + マンゴーの数/全体の数)2 + (グレープフルーツの数/全体の数)2}となります。
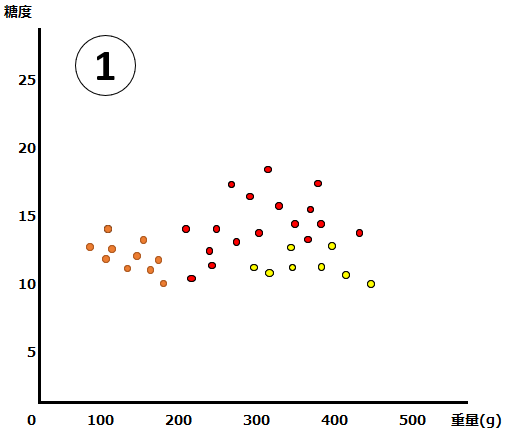
今回の例ではみかんが10個、マンゴーが17個、グレープフルーツが8個、全体で35個なので、以下のように計算できます。
gini =1-((10/35)2+(17/35)2+(8/35)2) = 0.63
この0.63が不純度です。完全に分類できている状態で0になるので、この状態では不純度が高い(分類されていない)と言えます。
次に②の状態におけるジニ不純度を計算します。計算方法は以下の通りで、分類後のそれぞれのカテゴリー内の不純度の加重平均で、(緑カテゴリーの数/全体の数) x { 1 – {(みかんの数/全体の数)2 } + (青カテゴリーの数/全体の数) x { 1 – マンゴーの数/全体の数)2 + (グレープフルーツの数/全体の数)2}となります。

計算としては以下の通りで、不純度は0.31に改善しました。
gini =(10/35)*(1-(10/10)2)+(25/35)*(1-((17/25)2+(8/25)2)) = 0.31
次に、③・④・⑤のどれが最もジニ不純度が低いのか(うまく分類できているか)を計算してみます。
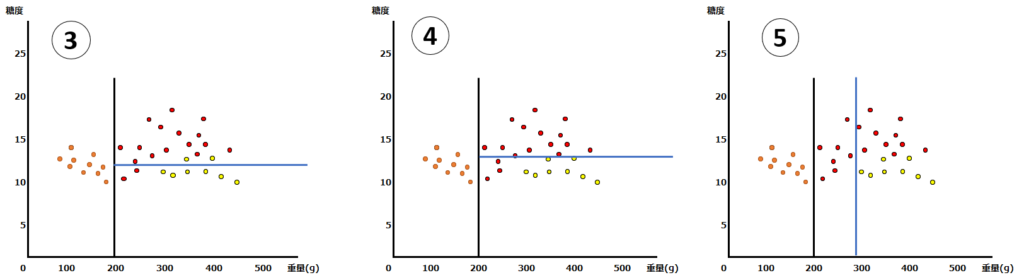
上の通り、④が最も不純度が低いことがわかりますので、④を選択して次に進みましょう。
③:(10/35)*(1-(10/10)2) + (17/35)*(1-((15/17)2+(2/17)2)) + (8/35)*(1-((2/8)2+(6/8)2)) = 0.19
④:(10/35)*(1-(10/10)2) + (14/35)*(1-(14/14)2) + (11/35)*(1-((3/11)2+(8/11)^2)) = 0.12
⑤:(10/35)*(1-(10/10)2)+(8/35)*(1-(8/8)2)+(17/35)*(1-((8/18)2+(9/18)2)) = 0.27
④の次に、”重量280g超かどうか”を条件にした緑線を引いたものを⑥としました。

不純度は以下の通り、0にすることができました。これで、完全に分類が完了しました。
gini =(10/35)*(1-(10/10)2)+(14/35)*(1-(14/14)2)+(3/35)*(1-(3/3)2)+(8/35)*(1-(8/8)2)) = 0
決定木では、上記のように不純度が最も低くなるように分類が進むのが特徴です。なお、この不純度の最小化は、”情報利得の最大化”と表現されることもあります。同じことを言っていますのでご留意ください。。
メリット・デメリット
上述の決定木には以下のようなメリットとデメリットがあります。
メリット
- データの前処理が不要(スケールを事前に準備する必要がない)
- 安定して精度が高い
- 分析結果を説明しやすい。
- (学習完了後の)予測が非常に高速
デメリット
- 全ての不純度を計算するため学習時の計算コストが高い
- 過学習を起こしやすい
過学習については以下の記事を参照ください。



コメント