今回は、ディープラーニングを学習するうえで理解が不可欠な活性化関数について説明します。ディープラーニングの基礎であるニューラルネットワークについては以下の記事を参照ください。
活性化関数とは何か
活性化関数(Activation function)とは、ニューラルネットワークの中間層において入力を別の形で出力するための関数です。詳しくは後述しますが、具体的にはSigmoid関数、SoftMax関数、tanh関数、ReLU関数などがよく使われる活性化関数です。
活性化関数の役割
ここからは、前回のパーセプトロンの内容を踏まえて活性化関数の役割を説明します。パーセプトロンの記事は以下から参照ください。
以下はパーセプトロンの記事で紹介した図を少しだけ変えた図です。Xとバイアスの1が入力、wは重みパラメータとしたときに、重みづけられた入力の総和であるa(W0+W1X1+W2X2)のことを”重み付け和”と呼びます。
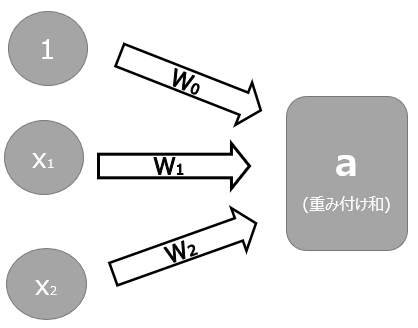
前回説明したパーセプトロンの話と異なるのはこの先の部分です。重み付け和aを、何らかの関数を使ってbに変換します。ここで使われる関数が、活性化関数です。
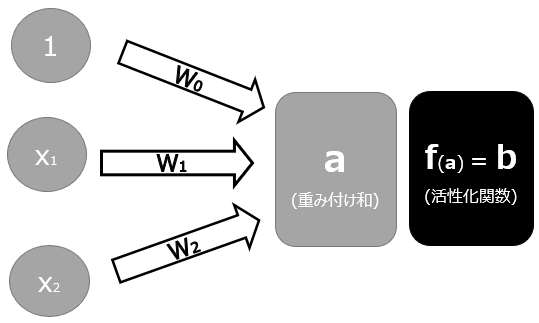
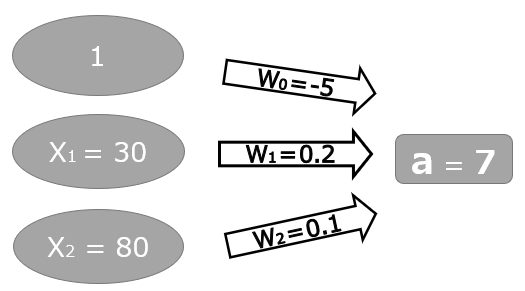
イメージがしやすいように具体的に数値を設定してみましょう。説明変数と重みパラメータは以下の図の通りです。
重み付き和aは1 x -0.5 + 30 x 0.2 + 80 x 0.1 = 7です。活性化関数は、この重み付き和の7を変換します。
例えば、活性化関数f(a)=a2とします。これは言い換えると、重み付き和aの値を2乗した値をbとするということです。今回の例でいえば、a=7より、活性化関数f(7)=72=49ということになります。

もし活性化関数f(a)=√aだとしたら、重み付き和の値を1/2乗する(ルートをつける)ということです。今回の例でいえば、a=7より、活性化関数f(7)=71/2=√7ということになります。
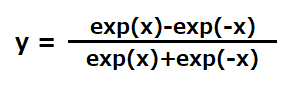
以上のように、重み付き和aに何らかの変換を加えるための関数が、活性化関数です。
なぜ活性化関数が必要なのか
では、なぜディープラーニングにおいて活性化関数が用いられるのかを説明します。
パーセプトロンの記事でも説明した通り、ニューラルネットワークでは単層パーセプトロンを多層にすることで、単層より複雑な変換を可能とします。一方で、パーセプトロンで行われる変換は、単層であれ多層であれ、どこまでいっても一次関数です。一次関数ということは、結局直線による分離(2変数なら平面による分離)しかできないということになります。
多層パーセプトロンが一次関数だということは、パーセプトロンの記事で紹介した重みづけられた入力の総和(重み付け和)”W0+W1X1+W2X2“を、見慣れた形であるz=ax+by+cと考えるとわかりやすいと思います。1変数関数であれば中学の教科書で登場するy = ax + bです。多層パーセプトロンの本質は、z=ax+by+cの形の処理を多く実行することです。
ディープラーニングは、ニューラルネットワークによって人間の脳のような複雑な処理の実現を目指します。しかし、多層パーセプトロンによって一次関数の処理をどれだけ重ねても、複雑さは一定の域を出ません。そこで、上述の重み付け和を、何らかの活性化関数を使って変換することで、一次関数では実現できない複雑な変換を可能にするのです。
関数の具体例
では次に、具体的にどんな関数が活性化関数として用いられるのかを紹介します。ここでも紹介する活性化関数は、ディープラーニングのために考え出された関数ではなく、元々知られていた関数が、ディープラーニングの活性化関数に使うのに便利だということで、慣習的に使われることが多い関数であるという点にご注意ください。
Sigmoid(シグモイド)関数
Sigmoid関数は、入力がx、出力がyの時に以下の式で表される関数です。

関数の特徴としては、以下のようにxの値がどれだけ大きくても小さくても、yの値が0-1の間に収まります。またx=0の時にy=0.5を取ります。入力xに関わらず出力が0-1の間の値を取ることから、2値分類の確率を出力する関数としても使われます。活性化関数の目的である非線形(直線ではない)の変換が実現できていることが見て取れると思います。
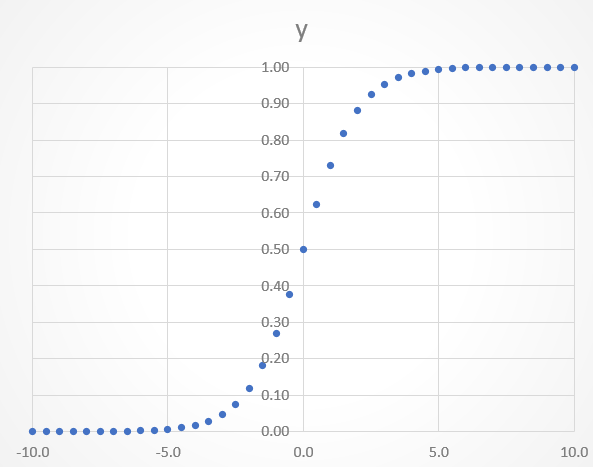
もう少し具体的に見てみましょう。exp(-x)というのは、ネイピア数eの-x乗という意味です。分母がネイピア数eのマイナスx乗というのが想像がつきにくいと思いますが、ネイピア数というのは約2.72のことです。文系出身者でもイメージが付きやすいように2の累乗だったらどうなるかを考えると、22=4、21=2、21/2=√2、20=1、2-1=1/2、2-1=1/4、となります。
以下に、入力値xが-10~+10の間の時に、ネイピア数eのx乗であるexp(x)、及びx乗を-x乗に変換したexp(-x)、そしてSigmoid関数変換後のyがどういった値を取るかを表にまとめいます。上述の説明で直感的にイメージがし難い場合の参考としてください。

SoftMax関数
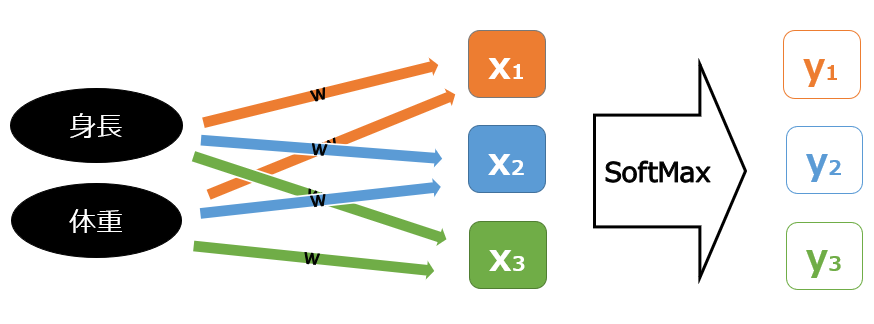
SoftMax関数は、入力と出力が1つずつであるSigmoid関数を、複数の入出力に応用した関数です。入力xが3つ、出力yが3つの時には以下の式で表されます。

出力が3つの問題というのは、例えば身長や体重などを説明変数に、服のサイズS(y1)/M(y2)/L(y3)の確率を出力するような多値分類の問題を想定するとイメージしやすいと思います。身長や体重の値に重みをかけた重み付き和が3つ(X)あり、それぞれSoftMax関数を適用します。
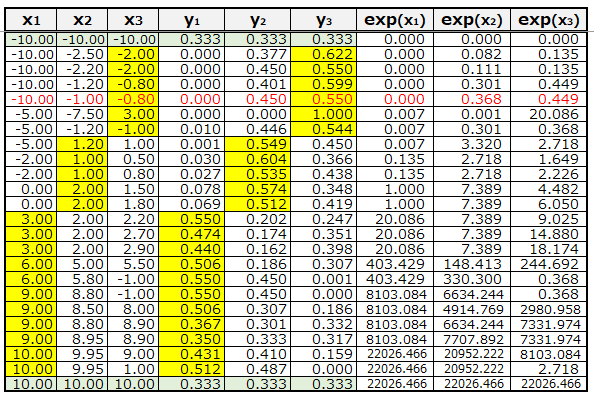
Sigmoid関数と同じくexp(x)用いて、出力地が0-1の間の値を取るような関数になっています。これが多値分類に活用しやすいのは、y1/y2/y3のそれぞれの0-1の間の出力地の合計が必ず1になるので、上記の問題設定でいえば、”Sの確率が5%、Mの確率が65%、Lの確率が30%”のように、多値分類の各分類クラスの確率値を出力してくれる点です。
具体例を見てみましょう。以下の表にて入力Xを-10~+10の範囲で適当な数字を置きました。薄緑色の最上段と最下段は入力値が同じ、上記の例でいえば服のサイズがS/M/Lの確率が同じのため、SoftMax関数適用後のyは、すべて0.333、つまりS/M/Lが33.3%ずつという結果になります。
また、例えば赤字にした5行目を見ると、X1に対してX2とX3は比較的値が近くなっています。出力値もy2は0.45、y3は0.55と近い数字になっており、X1はほぼ0となっています。これを服のサイズの問題に置き換えるなら、身長と体重からするとSサイズではなさそうだが、M/Lはどちらもあり得て、どちらかと言えばLサイズの確率が高い、と読み替えることができます。
tanh関数
tanh関数(Hyperbolic tangent関数、双曲線正接関数)は、入力がx、出力がyの時に以下の式で表される関数です。
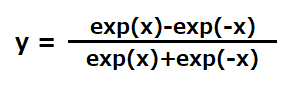
関数の特徴としては、以下のようにxの値がどれだけ大きくても小さくても、yの値が-1~1の間に収まります(Sigmoid関数は0~1)。x=0の時にy=0を取ります。

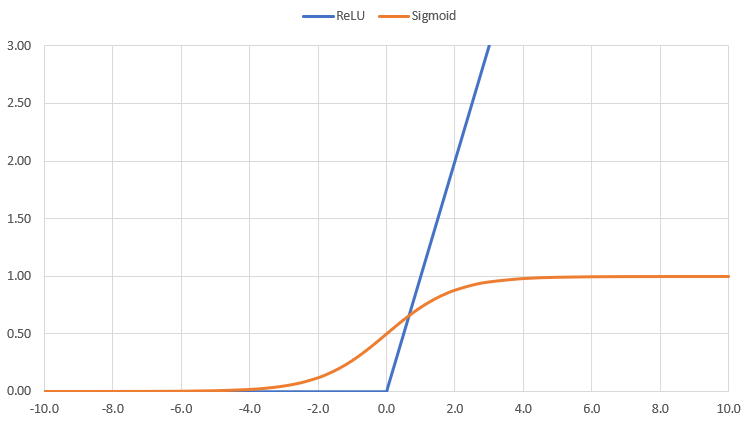
微分した値が最大で1となる、マイナスの値も出るというところがSigmoidと異なります。Sigmoidとの出力の違いは以下のグラフを参照ください。こういった出力値や傾き値の違いによる特性ゆえに、LSTMやAttentionなどの機構でtanh関数が使われています。

ReLU関数
ReLU(Rectified Linear Unit)関数は日本語では正規化線形関数です。今後詳細記事を掲載しますが、誤差逆伝播における勾配消失問題を解決するために、活性化関数として用いられるようになりました。計算式は以下の通りで、0と入力値とどちらか大きい方を返すという関数です。
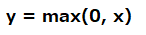
グラフにすると以下の通りで、入力Xが0を下回っている間は、どんな入力値でも出力は0です。一方入力が0以上の時は、入力xがそのまま出力yの値になります。
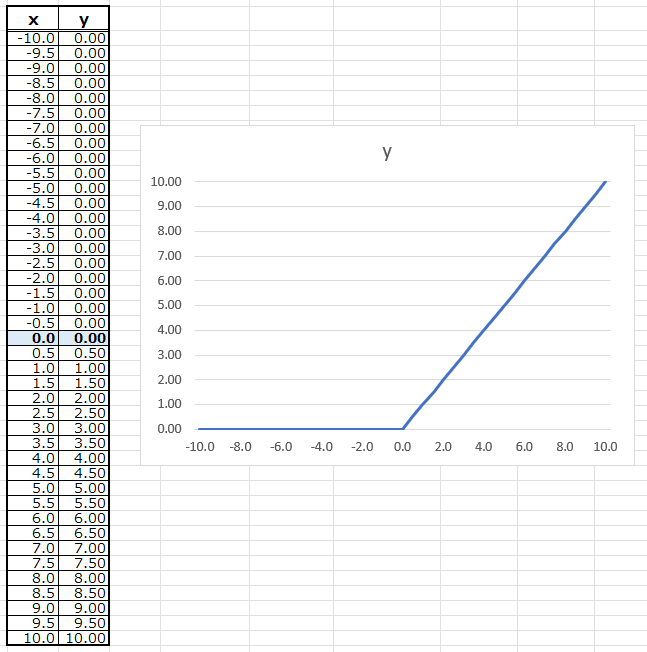
Sigmoid関数との比較は以下を参照ください。


コメント