今回は学習の中の教師あり学習の分野における、パーセプトロン(Perceptron)について解説します。機械学習の概要や基本的な用語の説明については以下の記事を参照ください。
パーセプトロンとは何か
重み付け和
パーセプトロンというのは、複数の入力信号を受け取ってそこから1つの出力をするアルゴリズムです。以下がパーセプトロンの基本構造です。まず複数の入力(以下では1,x1,x2の3つ)のそれぞれに対し、重みづけ(wで掛け算)を行います。入力の合計値としてX0+W1X1+W2X2と表されるものを、重みづけがされた総和という意味で、”重み付け和”と呼びます。
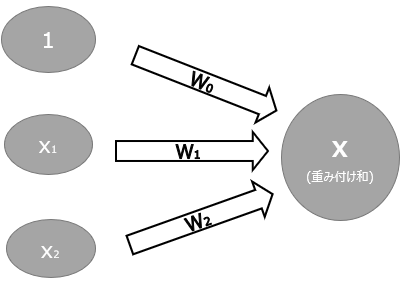
また、パーセプトロンでは閾値などを設定することで0又は1を出力することができます。そうするとパーセプトロンは以下の通り、入力部分、入力を受け取るニューロン、出力部分から構成されることになります
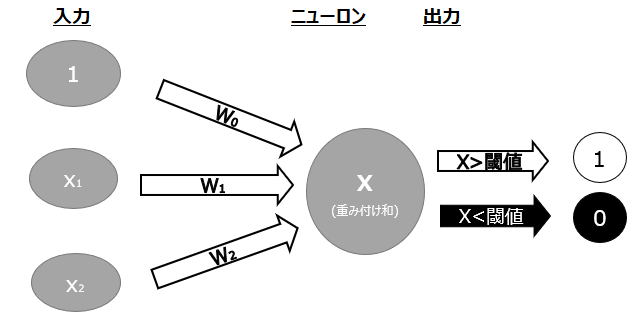
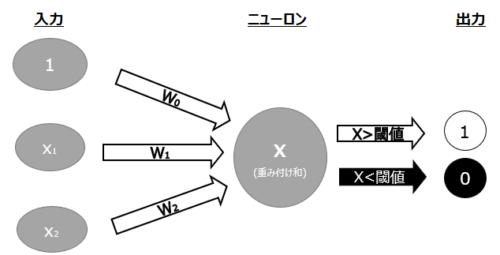
閾値を設定する場合は、重み付け和をニューロンで受け取った後、出力部分では予め決められた閾値と比較し、その結果によって出力を変えることができます。例えば入力の総和が閾値よりも大きければ出力が”1”となり、小さければ”0”というイメージです。
直感的な説明をするなら、人間が視覚的に捉えている情報について、例えばトラックが猛スピードで進む映像は重み付けが大きく、出力されやすい(認識されやすい)情報としてニューロンで処理されますが、ガードレールに黒い染みが付いている映像は重み付けが小さく、出力されにくい(認識されにくい)情報としてニューロンで処理される、というイメージです。
以下では、より具体的にパーセプトロンについて説明します。
単層パーセプトロン
上記で説明したパーセプトロンを1つだけ用いるのが単層パーセプトロンです。ここでは、気温と湿度から熱中症になるかどうかを予測する仮想のモデルを考えてみましょう。
説明変数1は気温、説明変数2は湿度です。”1”というのはバイアスと呼ばれるもので、1次方程式でいう切片のようなものだとイメージしてください。以下ではそれぞれ重みW0、W1、W2を設定しています。このパーセプトロンの閾値を0.6に設定した時、このモデルはどのように動くでしょうか。

例えば”気温25度、湿度15%”であれば、(1 x -0.5) + (25 x 0.02) + (15 x 0.01)=0.15(15%)となり、閾値の0.6(60%)を下回る為、出力は0、つまり”熱中症にはならない”と予測します。
例えば”気温35度、湿度50%”であれば、(1 x -0.5) + (35 x 0.02) + (50 x 0.01)=0.7(70%)となり、閾値の0.6(60%)を下回る為、出力は1、つまり”熱中症になる”と予測します。
これが単層パーセプトロンです。
単層パーセプトロンの本質は線形分離
上述のように、重みづけられた入力の総和はW0+W1X1+W2X2で表されます。仮にバイアスがなければ、W1X1+W2X2です。この値が閾値を超えるかどうかで出力が決まります。以下は上図の再掲です。

閾値をθとすると、W1X1+W2X2=θについて、それより大きいかどうかで判定するということです。これ変形すると、W1X1+=-W2X2+θです。試しにW1=1,W2=1,θ=1.2とすると、以下のようになります。この直線より下の黒点を1、白点を0と出力します。
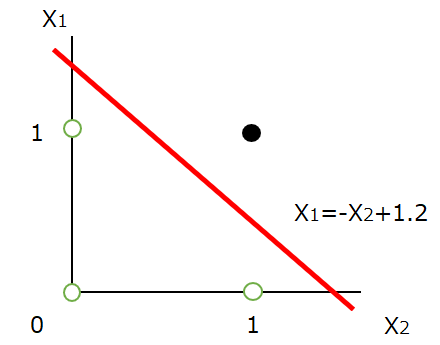
このグラフからも直感的に理解できると思いますが、単層パーセプトロンの本質は線形分離なのです。ここに、単層パーセプトロンの限界があります。
単層パーセプトロンの限界
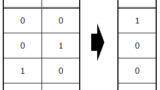
上のグラフでの線形分離結果をまとめると以下のようになります。

これは、論理演算でいうAND(論理積)です。他にも、単層パーセプトロンを使ってOR(論理和)や、NAND(否定論理積)、NOR(否定論理和)の線形分離が可能です。論理演算については以下の記事を参照ください。
一方、単層パーセプトロンでは表現できない論理演算の1つが、XOR(排他的論理和)です。XORの変換をすると、出力は以下のようになります。

これはグラフ上では以下のようになり、1本の線では分離できません。

このように、線形分離できる変換処理しか実現できないことが単層パーセプトロンの限界です。
多層パーセプトロン
上述の様に単層パーセプトロンには限界がある為、単体では強力なモデルではありません。しかし、パーセプトロンを2層以上繋げる多層パーセプトロンは上記の限界を乗り越えており、またその構造はディープラーニングで用いられるニューラルネットワークの基礎中の基礎になっています。
多層パーセプトロンについては以下を参照ください。



コメント