機械学習において最も重要なポイントの一つが、いかにして最適なパラメータ(w)を見つけるか、ということです。y=w0+w1xにおけるw0やw1、見慣れた形であればy=ax+bのaやbがパラメータですが、その最適値を見つけるにあたり重要な事項である最小二乗法や平均二乗誤差(MSE)について解説します。
最小二乗法
最小二乗法というのは、誤差のあるデータの集合に対して最も確からしい関係式を求める際に、誤差の二乗の総和が最小になる様にする手法です。
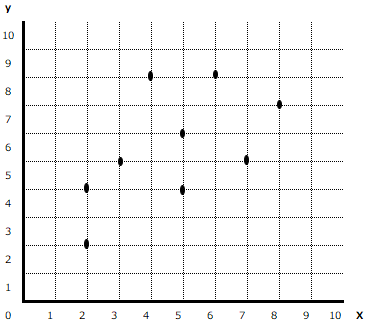
例えば以下のようなデータの集合を考えてみましょう。x,y座標上に、10個の点があります。これらのデータに対して、最も確からしい関係式を表す直線を引くとしたら、どのように引けばいいでしょうか。
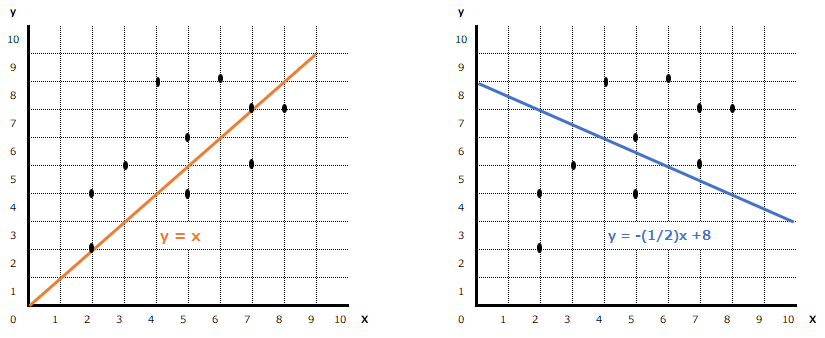
例えば以下のように、オレンジ色のy=xという直線を引く場合と、藍色のy=-(1/2)x+8という直線を引く場合、どちらの方がより確からしい関係式だと言えるでしょうか?
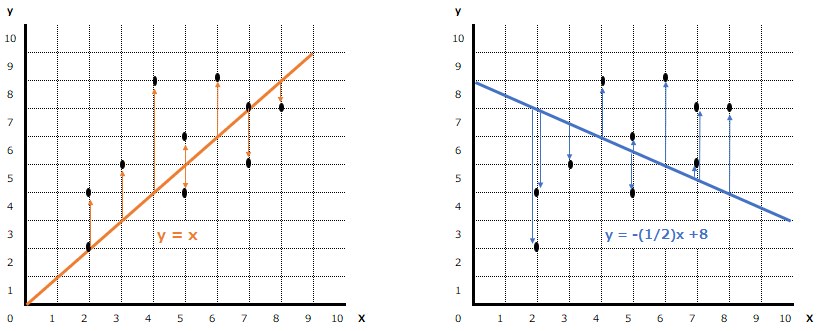
最小二乗法というのは、確からしさを判定するために、以下のように直線と各データの距離を測ります。この距離を、関係式と各データの”誤差“と呼び、その誤差の合計が最も小さい直線を、最も確からしい、と判定するのです。
残差平方和と平均二乗誤差(MSE)
では実際に誤差を計算してみましょう。10個のデータを以下のようにナンバリングした時、

上記の二つの直線と各データの誤差(距離)はそれぞれ以下のようになります。
- 関係式 :1の誤差、2の誤差、3の誤差,,,,10の誤差
- y = x : 0,2,2,-1,1,4,2,0,-2,-1
- y = -(1/2)x+8 : -5,-3,-1.5,-1.5,0.5,2,3,2.5,0.5,3
これで、それぞれの誤差が求められましたが、このままではプラスの誤差とマイナスの誤差が混在しており、そのまま足したり平均したりしてしまうと、プラスとマイナスで誤差が相殺されてしまう可能性があります。例えば直線①の誤差が+1と-1、直線②の誤差が+5と-5であれば、本来誤差が少ない直線①の方が誤差が少ないと判定されるべきですが、誤差をそのまま足してしまうと、2つの直線の誤差が+/-0で同じになってしまいます。
そういった事態を避けるために最小二乗法において用いられるのが、最小二乗誤差です。これは、関係式と各データの誤差を二乗することでプラスマイナスの影響をなくし、その上で二乗した誤差をすべて足し合わせて、二乗誤差の総和が最も小さいものを、最も誤差が小さいと判定する方法です。上述の2つの直線の二乗誤差の総和は、それぞれ以下のようになります。
- 関係式 : 二乗誤差の総和(各二乗誤差)
- y = x : 35(0,4,4,1,1,16,4,0,4,1)
- y = -(1/2)x+8: 67.25(25,9,2.25,2.25,0.25,4,9,6.25,0.25,9)
このとき、こういった二乗誤差の総和のことを残差平方和と呼び、二乗誤差の平均値のことを平均二乗誤差(Mean Squared Error, MSE)と呼びます。残差平方和や平均二乗誤差が小さいほど、より確からしい関係式であると言えます。
こうして、オレンジの直線の方がより確からしい関係式であることを判定できました。

最小二乗誤差
上で見たように、二乗誤差の総和によって2つの直線のどちらがより確からしいか判定することができました。では次に、あらゆる直線の中でどの直線が最も確からしいか、言い換えると、直線の最適なパラメータ(ここでは切片と傾き)をどのように求めればいいかという話に進みます。
最適なパラメータの算出方法には解析的に解く方法と、数値的に解く方法の2種類があります。
解析的に解く(正規方程式)
解析的に解くというのは、式の変形によって解を求めることです。例えばy=2x+3かつy=x+8の時、式の変形によってx=5、続いてy=13と求めることができますが、これが解析的に解くということです。
解析的手法として正規方程式が挙げられます。正規方程式を解く場合には厳密な解が得られる一方で、常に解が得られるとは限りません。また変数が多い場合には計算するのがとても大変になります(計算コストが高い。)。
数値的に解く(勾配降下法)
数値時に解くというのは、具体的な値を代入し続けて近似的な解を得る手法です。例えばy=2x+3かつy=x+8の時、xやyに値を適当に代入して、成り立つかどうかを1つずつ試していくようなイメージになります。
数値的に解く手法の代表例が勾配降下法です。勾配降下法は、解に誤差が生じる可能性がある一方で、ほとんどの場合で解を求めることができます。勾配降下法については以下の記事を参照ください。

コメント