今回は、機械学習やディープラーニングで精度の高いモデルを作成する際に欠かせない、正規化について説明します。
正規化とは何か
正規化(nomalization)というのは、様々なデータを同時に扱うときに、扱いやすいようにデータの尺度を統一することです。
例えば大学入学共通テスト(以前はセンター試験)の英語の点数とTOEICの点数から、東京大学の英語の点数を予測するモデルを作成するとします。この時、大学入学共通テストの満点は100点(センターは200点)ですが、TOEICは990点です。配点が異なるので、これらを以下のいずれかの方法で同じ尺度に直すのが正規化です。
一般に正規化というと、最小値を0、最大値を1として、データを0~1の中でスケーリングすることを指すことが多いです。この手法は正規化の中でもmin-Max normalization(最小最大正規化)とも呼ばれ、データの最小値と最大値が明確になっているデータに適しています。後述の例でもこの手法を前提に説明します。
なお。0~1の範囲で正規化するには、以下のような計算をします。
正規化された値 = (あるデータの値 – データの最小値) / (データの最大値 – データの最小値)
標準化 (Z-score normalization)
正規化の手法の1つに標準化(Standardization)があります。標準化は平均0、標準偏差1としてスケーリングする手法です。Z-score normalizationとも呼ばれます。大きな外れ値がある場合や、データが正規分布している場合には、標準化が有効な場合があります。
外れ値というのは、データ集合の中で他の値から大きく離れた、または予期しない程度に異なる値のことを指します。直感的に説明するならば、平均点40点、95%の人が30-50点のテストで100点に近い点数を取った場合の点数のデータや、気温に応じてアイスクリームの販売数量が増えるはずなのに、特殊要因である1日だけ以上に販売数量が増えた日の販売数量のデータは外れ値となりえます。
なお、”z-score“や”標準化”という言葉は統計学に由来します。統計学では平均0、標準偏差1の正規分布のことを標準正規分布と呼び、標準正規分布に従う変数をしばしば”Z”と表記します。正規化の中でも特に標準正規分布に従うように変換する手法なので、標準化、およびz-score normalizationと呼ぶのです。標準化は以下のように計算されます。
標準化された値 = (あるデータの値 – データの平均値) / データの標準偏差
なお標準偏差や正規分布については以下を参照ください。
正規化と標準化の違い
では正規化と標準化は何が違うのでしょうか。0~1の範囲、もしくは平均0で標準偏差1の範囲に正規化するという、わざわざ別の手法が存在する理由はなんでしょうか。
標準化の項目でも説明した通り、標準化は外れ値に強い手法です。このことを視覚的に理解してみましょう。以下のように、平均30点、標準偏差10点のテストがあったとします。この時、一人だけ80点の人がいたとしましょう。これが上で言う外れ値です。
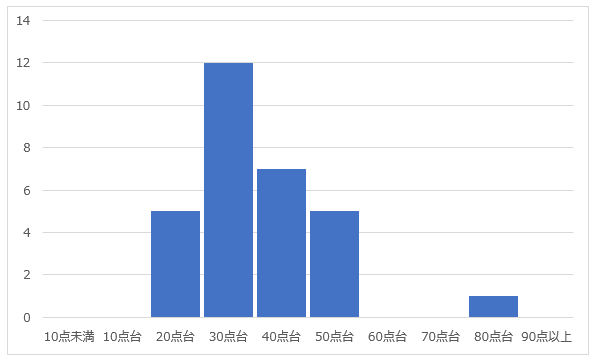
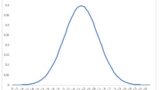
このテストの点数を0~1で正規化すると、分布は以下の通り、外れ値に引っ張られて中心が大きく左にずれています。ほとんどのデータが0.5以下になっていることも見て取れます。
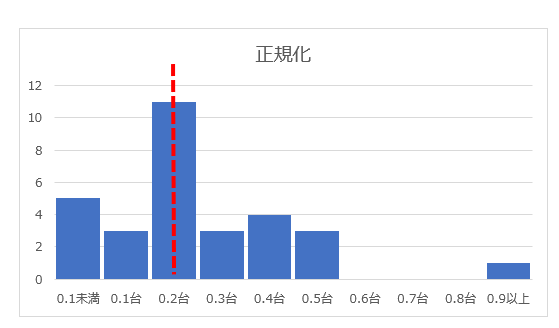
一方平均0で標準偏差1となるように標準化すると、以下のようになります。平均0なので当たり前ですが、0付近にデータが集まっているので扱いやすく、また外れ値が特異であることも認識できます。
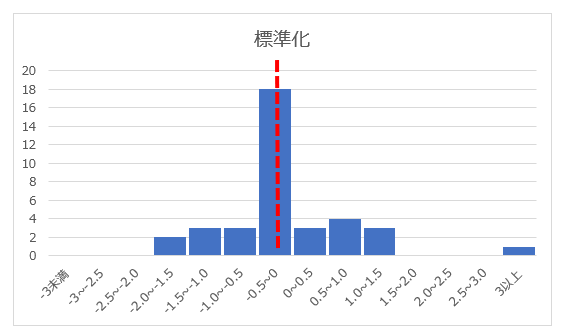
なぜ正規化が必要なのか
次に、なぜそもそも正規化という作業が必要なのかを説明します。
正規化しない場合
正規化が必要な理由は、一言でいうならば、正規化をせずにデータを用いると、スケール(尺度)の小さなデータがスケールの大きなデータに引っ張られて、影響が小さくなってしまうからです。
例えば、AさんからEさんの共通テスト、TOEIC、東大入試の点数が以下のように分布していたとしましょう(適当な数値です)。今回は故意的に、共通テストと東大入試の点数の相関が強く、TOEICと東大入試の相関が弱いような点数を設定しています。
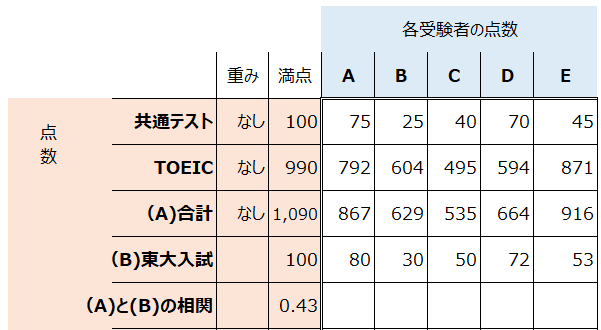
“(A)と(B)の相関”というのは、相関係数の値です。相関係数が0.41なので、正の相関はあるが、弱い相関と言え、この相関では東大入試の点数を予測するモデルを作成しても精度が高くなるのか疑問です。共通テストの点数を東大入試の点数の相関が高くても、点数配分の大きく相関の小さいTOEICの点数と一緒に合計してしまっているために、TOEICに引っ張られて、全体として相関が小さくなってしまいました。
なお相関係数というのは、2つのデータの相関の強弱や正負を示します。0が最も相関がなく、1が最も強い正の相関、-1が最も強い負の相関です。0.7を超えてくると相関が非常に強く、反対に0.2を下回るとほとんど相関がない、と判断されます。負の値でも同じです。
正規化する場合
上記の点数を上述のMin-Max normalizationの手法で正規化すると、以下のようになります。正規化後の点数は、(元の点数 – 最小値)/(最大値 – 最小値)で計算され、最大で1、最小で0になるように調整されます。

正規化によって、相関が強い共通テストの影響が正しく評価され、全体としても相関係数が0.82となり、東大入試の点数との間に強い相関が見て取れるようになりました。
相関係数が0.43と0.82というのは、予測モデルを作るかどうかの判断に大きく影響を与えるくらいの大きな差です。正規化という作業をするだけで、予測モデルを構築できる可能性が大きく高くなることが示唆されます。



コメント