今回は機械学習の中の教師あり学習の分野における、線形回帰について解説します。機械学習の概要や基本的な用語の説明については以下の記事を参照ください。
線形回帰とは何か
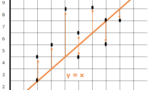
線形回帰というのは、一言でいうと1本直線を引くことで予測することのできる問題です。例えば以下のように、気温とアイスクリームの販売数量に関するデータが合ったときに、

以下のように直線を1本引くことでその関係性を説明できるならば、“30度の日は100個売れるだろう”といった具合に、気温がわかればアイスクリームの販売数量を予測することができます。
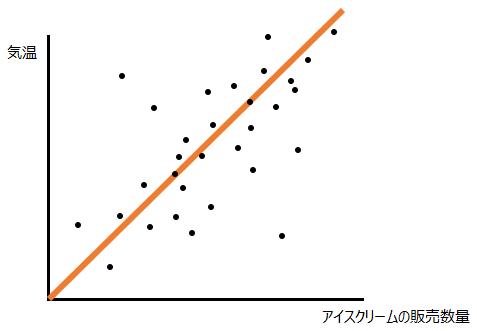
線形回帰の種類
単回帰モデル
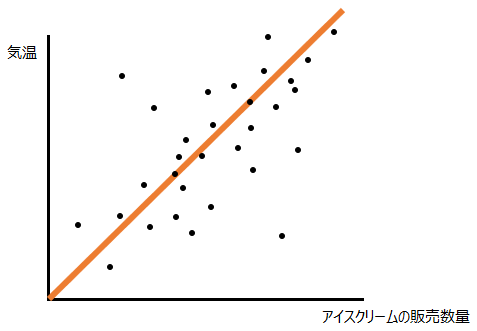
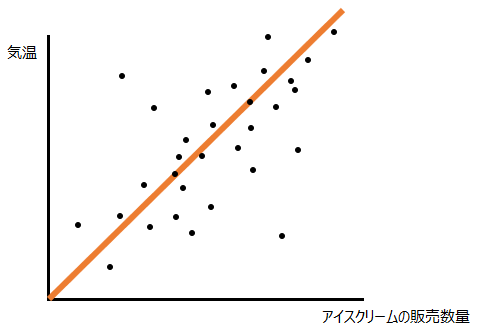
単回帰モデルは、線形回帰モデルの中の、いわゆる直線で表すことができる、説明変数が1つの1次関数のモデルです。一般的にはy=ax+bの形で馴染みがあると思いますが、機械学習の分野ではアルファベットの代わりに重み(weight)・パラメータを表す記号wが使われますので、ここでもy=w0+w1xとさせてもらいます。上でも出てきた以下の直線はy=w0+w1xの例として理解しやすいでしょう。
多重線形回帰モデル
多重線形回帰モデルとは、線形回帰モデルの中の、説明変数が複数ある線形回帰のモデルです。現実世界の予測問題で、1つの変数で説明ができる問題は多くありません。例えばアイスクリームの販売数量を気温だけでなく湿度も用いて2つの変数から説明すれば、それは多重線形回帰モデルとなります。説明変数がn個の場合、以下のような式で表すことができます。
y=w0+w1x1 +w2x2 +w3x3 …+wn xn
非線形化
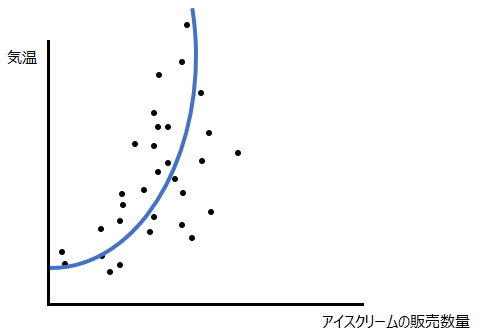
直線を生成するだけではうまくいかない時に、説明変数の2乗や3乗の値をモデルに組み込むことで非線形である高次関数を生成することで予測精度が高くなる場合があります。
パラメータの最適化
最小二乗法
機械学習において最も重要なポイントの一つが、いかにして最適なパラメータ(w)を見つけるか、ということです。y=w0+w1x1におけるw0やw1、見慣れた形であればy=ax+bのaやbがパラメータですが、その最適値を見つけるにあたり重要なのが最小二乗法です。詳しくは以下の記事を参照ください。
正則化
一方、最小二乗法で過学習が起きる場合は、正則化(regularization)という手法を用いることがあります。正則化というのは、適切な係数を取捨選択したり、係数の大きさを小さくすることによって過学習を防ぐ手法です。詳しくは以下の記事を参照ください。
線形回帰に正則化項を加えた手法として以下の2つが挙げられます。他の方法で精度が向上しない時に試してみてください。
Lasso回帰
Lasso(Least angle regression)回帰は、L1正則化を用いた縮小推定の手法です。
Ridge回帰
Ridge回帰は、L2正則化を用いた縮小推定の手法です。


コメント